金，决定租金的因素包括租赁设备的购置成本（由设备的买价、运杂费、途中保险费等构成，本文假定上述因素已综合考虑在租金总额中）、租赁设备的预计净残值（本文假定无残值）、利息、租赁手续费（本文假定已含在租金总额中）、租赁期限、租金的支付方式。租金计算方法主要有直线法、等额年金法、附加率法、浮动利率法。在我国融资租赁实务中，大多采用等额年金法，本文中模型以等额年金法为依据。

等额年金法是将一项租赁资产在未来各租赁期内的租金金额按一定的贴现系数予以折现，使其现值总额恰好等于租赁资产的购置成本。在这种方法下，通常要综合利率和手续费率确定一个租赁费率，作为贴现率，在模型中体现为租金年利率。等额年金法又可分为等额年金后付法和等额年金先付法两种。等额年金后付法是承租企业与租赁公司商定的租金支付方式，大多为后付等额租金，即普通年金。其计算公式为A=C/（C/A，i，n）。式中：A为每期支付租金；C为租赁设备购置成本或租金总额；（C/A，i，n）为n期后付年金现值系数，其中i为租赁费率即贴现率（租金年利率），n为支付租金次数。工作表函数为A=PMT（i，n，C）。等额年金先付法是承租企业采取先付等额租金的方法支付租金。其计算公式为A=C/[（C/A，i，n-1）+1]。各参数含义同上，其中，（C/A，i，n-1）+1为n期先付年金现值系数。工作表函数为A=PMT（i，n，C，0，1）。

二、每期应付租金计算静态模型设计

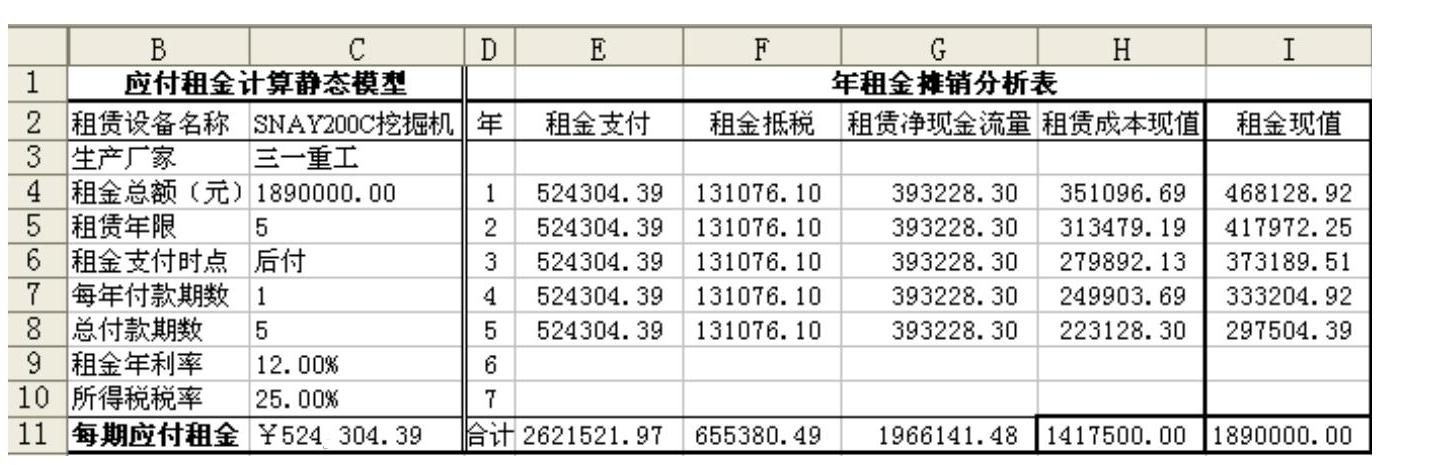
为阐明模型设计原理，笔者依据先易后难、由简至繁、逐步扩展的原则，先设计了从每期应付租金计算的静态模型（采用等额年金后付法，如图1所示）。设计过程假定无论设备价值高低，达到使用寿命时均无残值。图1中左边是应付租金计算的静态模型，右边是由静态模型进一步生成的年租金摊销分析表，目的是使静态模型更加完备，便于决策者全面了解该租赁项目现金流状况、掌握租赁成本现值，便于做出更为精准的决策。

模型中：每期应付租金=PMT（租年利率,总付款期数,-租金总额）；租金支付=每期应付租金×每年付款期数；租金抵税=E4×所得税税率；租赁净现金流量=E4-F4；租赁成本现值=G4/（1+租金年利率）^D4，或-PV（租金年利率，D4，G4）；租金现值=E4/（1+租金年利率）^D4，或-PV（租金年利率，D4，E4）。需要说明的是，为简化模型设计，方便读者掌握设计原理，租金总额已综合考虑了租赁设备的购置成本以及由出租人支付的设备的买价、运杂费、途中保险费、安装调试费等相关费用，输入该项数据时，应包含出租人支付的相关费用；租赁手续费已含在租金总额中；模型中假定设备无残值。若实际租赁业务中需要分项考虑，可以在此模型的基础上，分项列示和输入相关数据。

在应用该模型时，用户只需在C2：C10区域输入租赁项目的已知数据即可得到相应租赁项目的每期应付租金和年租金摊销分析结果，从而满足租赁决策需求。但同时，该静态模型存在如下问题：已知数据输入太繁琐；只能对每年年末付款的5年租赁项目进行分析，否则会出现数据错误，如对期初付款、每年2期付款、7年的租赁项目等情况，该模型均不能处理；年租金摊销分析表的行数不能随着租赁年限的变化而增减。为解决上述问题，笔者进一步设计了应付租金计算的动态模型。

三、每期应付租金计算动态模型设计

（一）设计思路

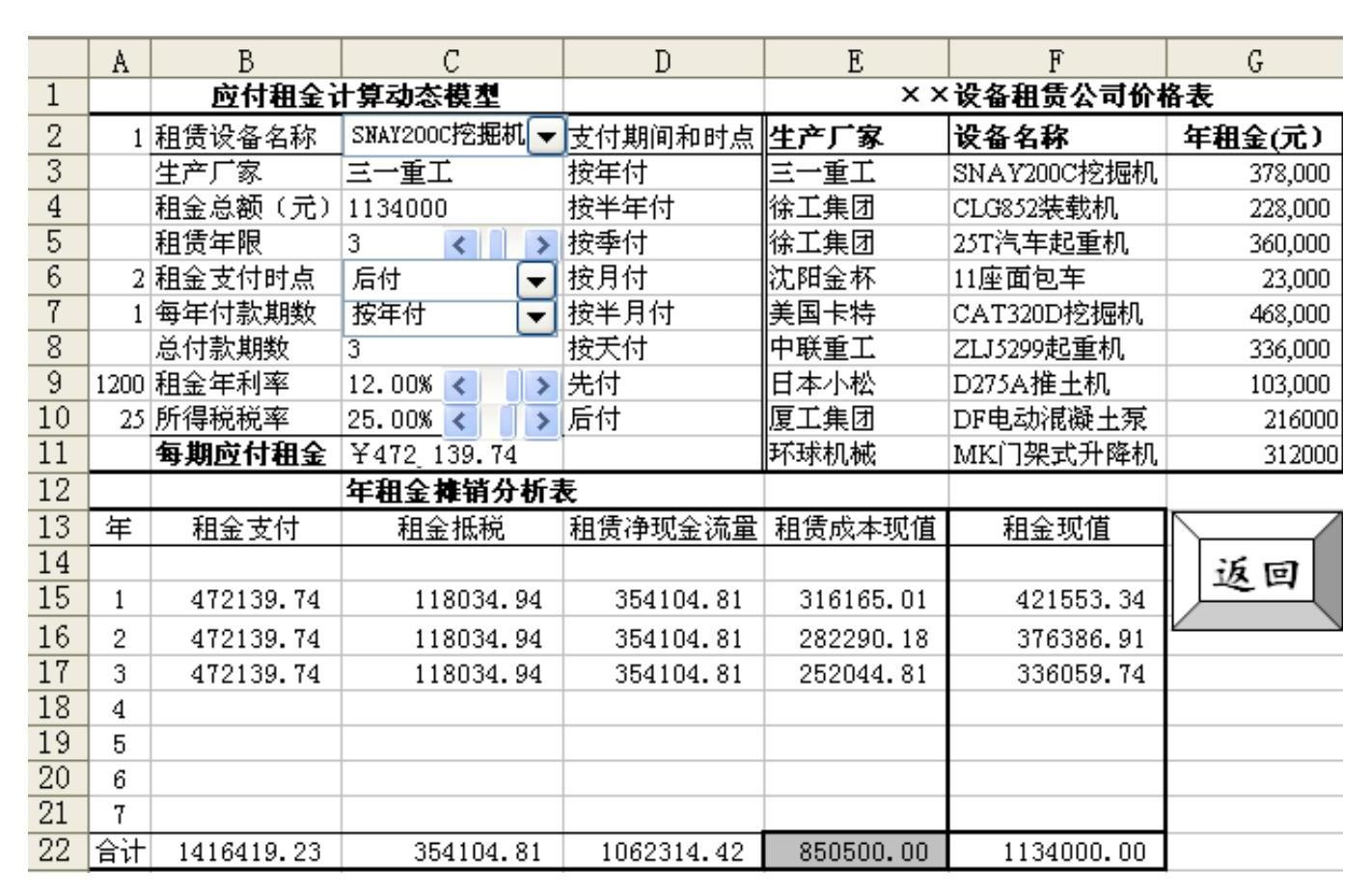
动态模型（如图2所示）的设计是按照“租赁项目、单独列表，已知数据、选择输入，分析表行、随需应变”的原则，将设备租赁项目及其价格单独划出一个区域，作为已知数据的数据源，方便用户选择输入动态数据；在“应付租金计算动态模型”的已知数据区域尽量根据数据特性使用“窗体控件”，如“组合框”和“滚动条”，一般来说，需要选择输入的数据可选用“组合框”，需要调节其值的数据宜选用“滚动条”；在“年租金摊销分析表”区域，可利用IF函数定义各个单元格公式，使该表能够“弹性伸缩、随需应变”。图2展示的是3年租期按年后付的年租金摊销分析表的瞬时数据。

（二）设计过程

动态模型的主要函数应用是INDEX函数、PMT函数、PV函数和IF函数；主要区域命名是“生产厂家”“设备名称”和“年租金_元”；主要窗体控件应用是“组合框”和“滚动条”。其中，“租赁年限”“租金年利率”“所得税税率”应用滚动条设计，只是设置控件格式中的最小值和最大值只能输入整数值，所以对“租金年利率”“所得税税率”要利用A9等单元格转换为图2中所示的百分数。主要公式的原理同静态模型。这种设计很大程度上提高了每期应付租金计算模型的通用性。

四、融资租赁与借款购入的分析比较模型设计

（一）融资租赁设备与借款购入设备的决策方法

该类决策方法主要有净利租赁现值法（NAL）、损益平衡租金法、租赁成本现值法三种。本文模型采用第三种方法。租赁成本现值法是通过计算融资租赁成本各期折现值合计与借款购入设备的资金本息各期折现值合计（即租赁成本现值与借款成本现值），选择成本现值较低的决策方法。

（二）决策模型设计

此处以成本费用现值法为例设计融资租赁决策模型。该模型是在每期应付租金计算动态模型（图2）的基础上，新增了“借款购入设备”的已知数据区域和“借款购入设备分期偿还分析表”区域，并在设备租赁公司价格表中加入“设备价值”一列（在计算折旧时要用到）。该模型的总体结构布局如图3所示。其他方面的设计思路和要点与应付租金动态模型的设计思路和要点类似。需要说明的是：在模型的“融资租入设备年租金摊销分析表”区域中各单元格中用IF函数定义的计算公式适用于成本费用现值法中融资租入设备时的租赁成本现值PLC）计算公式；在模型的“借款购入设备分期偿还分析表”区域的各单元格中用IF函数定义的计算公式适用于成本费用现值法中借款购入设备时的借款成本现值（PBC）简化计算公式；在新增的借款购入设备分期偿还分析表”区域，若每年还款期数大于1，则由于资金时间价值的存在，以PMT函数计算的年等额还款额要大于每期偿还金额乘以每年还款期数后的年偿还额。

该模型主要函数应用包括INDEX函数、PMT函数、PPMT函数、IPMT函数、AND函数、SLN函数、SUM函数、IF函数，主要区域命名、主要窗体控件与图2类似，不再赘述，主要公式的原理同动态模型。至此，融资租赁决策模型设计完毕。需注意，运行该模型时，借款购入设备与融资租入设备应是针对同一项目，根据谈判或决策需要，可随时调节动态控件的可变参数，在借款或租赁的相应分析区域即可实时得到分析结果和辅助决策结论。

责任编辑 李卓