摘要:
一、孤立点分析方法介绍
孤立点是在运用计算机进行数据处理过程中呈现离散状态的小规模数据对象,这一小部分数据对象与数据中的一般规律和趋势有着显著差异。孤立点分析主要利用数据挖掘理论模型和分析方法,发现数据在集中态势下所出现的异常值。对于审计分析来说,异常的数据、事件、频率等往往具有特殊含义或隐藏重要信息,可从中找到违法违规行为的线索。
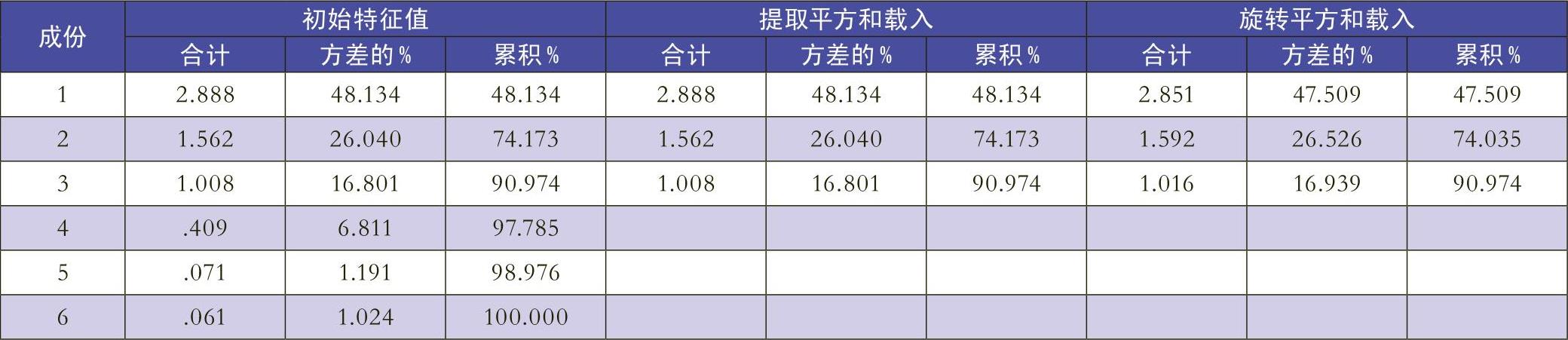
孤立点分析方法主要分为两个步骤:第一步,在给定的数据集合中先确定变量属性,即获取所需财务数据和非财务数据并进行分类,然后进行因子分析。因子分析是指从多个变量指标中选择少数具有代表性的综合变量指标,继而达到数据降维目的的一种多元统计方法。因子分析的主要模型为:X=AF+ε,其中,X代表原始数据指标,F代表X的公共因子,A代表因子载荷矩阵,ε为特殊因子。在因子分析过程中,首先通过解释总方差可获得累计方差贡献率,此指标越高表明公共因子对所有原始数据的代表程度越高,则公共因子的可信度越高;其次计算输出因子载荷矩阵(通常使用正交旋转成分矩阵表示),得到标准化的公共因子近似表示标准化的原始数据的系数矩阵,因子载荷矩阵中的元素数值越高表明公共因子对原始数据解释程度...
一、孤立点分析方法介绍
孤立点是在运用计算机进行数据处理过程中呈现离散状态的小规模数据对象,这一小部分数据对象与数据中的一般规律和趋势有着显著差异。孤立点分析主要利用数据挖掘理论模型和分析方法,发现数据在集中态势下所出现的异常值。对于审计分析来说,异常的数据、事件、频率等往往具有特殊含义或隐藏重要信息,可从中找到违法违规行为的线索。
孤立点分析方法主要分为两个步骤:第一步,在给定的数据集合中先确定变量属性,即获取所需财务数据和非财务数据并进行分类,然后进行因子分析。因子分析是指从多个变量指标中选择少数具有代表性的综合变量指标,继而达到数据降维目的的一种多元统计方法。因子分析的主要模型为:X=AF+ε,其中,X代表原始数据指标,F代表X的公共因子,A代表因子载荷矩阵,ε为特殊因子。在因子分析过程中,首先通过解释总方差可获得累计方差贡献率,此指标越高表明公共因子对所有原始数据的代表程度越高,则公共因子的可信度越高;其次计算输出因子载荷矩阵(通常使用正交旋转成分矩阵表示),得到标准化的公共因子近似表示标准化的原始数据的系数矩阵,因子载荷矩阵中的元素数值越高表明公共因子对原始数据解释程度越好,有利于对公共因子进行命名,从而得到降维后的数据指标。
第二步,检测和挖掘数据集合中呈现离散状态的小规模数据,即发现孤立点。目前传统方法主要采用基于统计、距离、偏差或密度的方法来寻找孤立点,而在云计算技术的支持下,可以通过系统设定更复杂的运算方法对所掌握的几乎无限的计算资源进行智能计算。
二、大数据环境下基于孤立点分析的审计抽样方法分析
高校基建工程结算审计所需资料文件多、非财务数据复杂多变、分析内容繁重,并且涵盖政策性和专业技术性问题。政府审计往往存在限于审计人员和时间相对不足,只能选取部分样本进行重点审计的情况。笔者以政府审计中的高校基建工程结算审计为例,演示基于孤立点分析方法的审计抽样模型的构建原理,并在此基础上进行具体案例分析。
(一)审计抽样模型构建原理演示
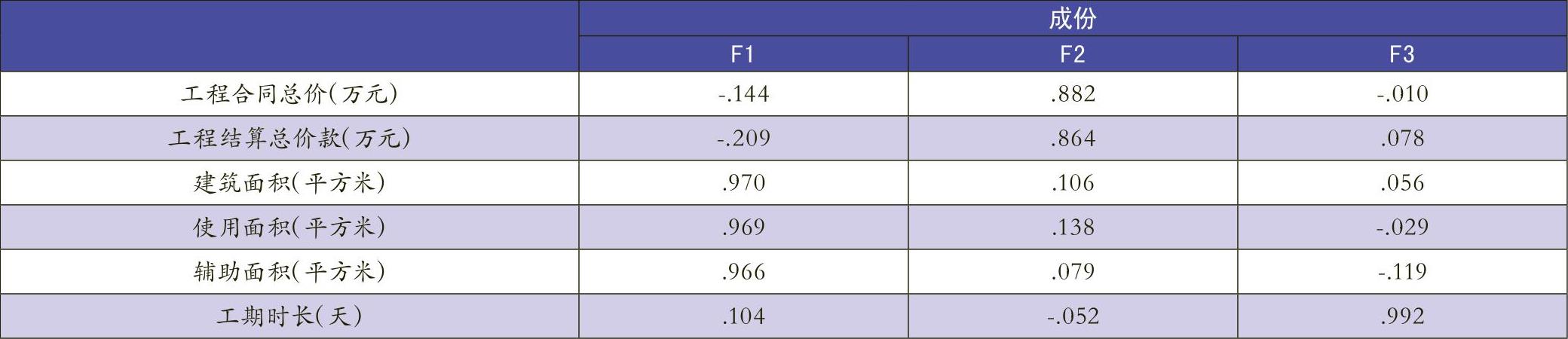
第二步,发现孤立点。笔者利用基于距离的孤立点分析方法,即使用K-means算法的聚类分析来寻找孤立点,目的是找出与宿舍楼建设综合情况相比差异较大的建筑项目,并利用因子散点图分析引起差异的原因所在。该算法的基本思想是:初始随机给定K个簇中心(K值根据实际情况设定),根据最邻近原则将待分类样本点分到各簇,并按平均法重新计算各簇质心,以确定新的簇心。一直迭代,直到簇心的移动距离小于某个给定的值,最终将K簇中包含观测点最少的一簇作为“孤立组”。根据上述的实际情况,认定若孤立组中包含的观测点数量占其总观测点数量的10%以下,则此孤立组包含的观测点被视为孤立点。此规则依据的是大部分观测点的聚集会使小部分“异常”观测点显现出来。之后利用三维因子散点图对所有数据进一步分析,可直观展现孤立点产生的原因。

(二)具体案例分析
近年来,随着招生规模的不断扩大,A市各高校均加紧基础设施建设,以保证学生的正常学习与生活。2005~2014年,全市25所高校共建成学生公寓178栋。为确保财政资金使用的安全有效,A市教委联合纪委、监察部拟对该市高校近十年来的新建学生公寓楼进行工程结算审计。限于人员和时间安排,不能对178栋公寓进行全面审计,因此拟基于孤立点分析进行审计样本的选取。
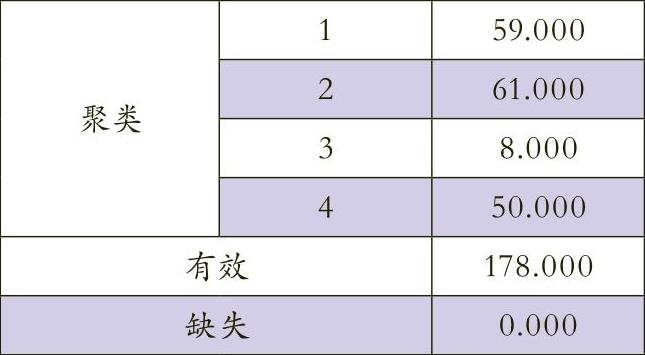
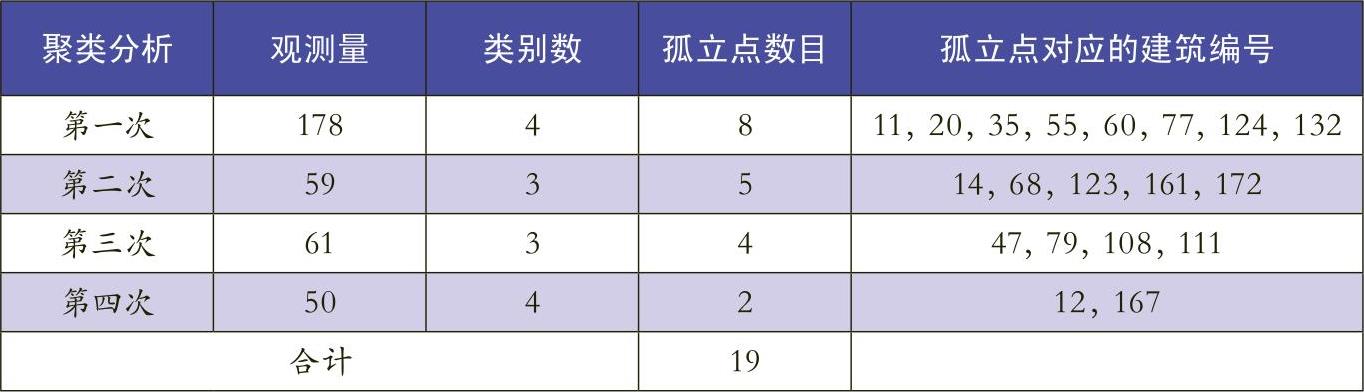
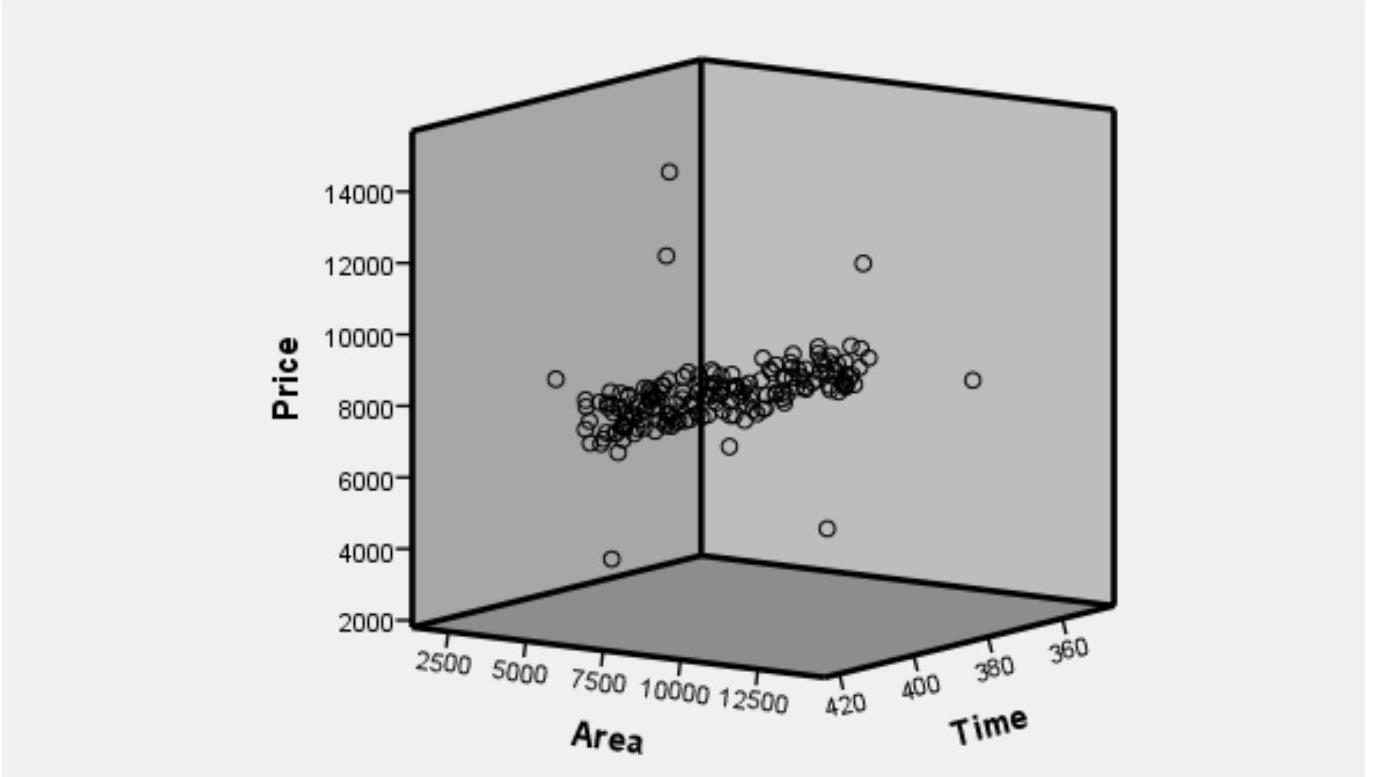
第二步,对以上3个公共因子进行K-means算法的聚类分析,以便寻找孤立点。在第一次聚类分析中,178组观测数据被分为4类(如表4所示),从中可以看出,所有记录没有缺失值,均有效。这个结果表明大部分数据间都是有相关性的,主要分布在1、2、4簇,只有第3簇的数据游离在其他数据之外。第三簇8个观测点占178观测点的4.5%,低于上文所述的10%,因此这8个观测点为孤立点。因为每个观测量所属类别及距离类中心的欧式距离已经作为新变量保存在数据表中,通过数据表中的类别变量,可得出这8个观测点对应的建筑编号分别是:11,20,35,55,60,77,124,132。为判断这8个孤立点所存在的问题,需利用三维因子散点图进行直观的反映(如图1所示)。因为Price、Area、Time3个变量是观测点的基础影响因素,笔者选择它们作为坐标轴,从中可以很容易地找到这8个孤立点,进而发现这8个点在价格或面积因素上明显偏离其他点。至此,通过一次聚类分析已经找到8个孤立点,但是仅以此作为审计范围显然不够,应通过多次迭代过程,以确保发现数据集中的所有孤立点。因此还需要对1、2、4簇中的观测点分别进行聚类分析。具体分析步骤与上文所述一致,不再重复。最后对四次聚类分析汇总结果(如表5所示),进而找到了19个孤立点,再将这19孤立点作为审计抽样的样本,结合因子散点图所示的偏差进行全面审计。
(本文受教育部人文社科<12YJC6301 81>、北京市哲学社科<13JGB047>、北京高校青年英才、国家社科基金<14AJY005和14ZDA027>、北京市教委创新团队和北京工商大学国有资产管理协同创新中心项目支持)
责任编辑 李卓
 京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号 京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号













