短期经营决策中经常遇到最优化决策问题，如多品种条件下的最优生产组合问题、最优定价决策问题、多目标决策问题、最优运输方案问题、最优选址问题、最优库存问题等。对于最优化问题，通常运用运筹学方法进行计算分析和决策。但该方法对于一般会计人员而言较为复杂且不容易理解，影响了最优化决策的效率。Excel为管理会计的最优化决策提供了方便的工具。本文将通过实例来设计最优化决策模型。因为前面文章已经对最优存货决策模型的设计进行过介绍，所以本文不再重述。

一、最优化决策的特征与建模要素

最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动，其目的是通过对问题的系统分析，进行人、财、物、时的优化配置，达到决策的最优目标。管理会计中的最优化问题大多为组合决策问题，如多品种的产品生产组合决策、多路径的运输路线决策、多地址的销售网点决策和生产厂址决策等。这些决策具有的共同特征是：

第一，多目标特征。最优化决策往往具有多种目标，且目标之间存在一定程度的不相融性或矛盾性，如利润最大、工时最少的决策。正是这种不相融和矛盾才使得最优化决策显得尤为重要；

第二，多资源特征。最优化决策通常面临多种资源的综合利用与优化配置；

第三，资源约束特征。无论是产品组合决策、定价决策，还是运输决策，都面临资源有限的约束，最优化决策正是要在资源有限的条件下达到最优目标，这些资源包括物质资源、货币资源、人力资源、时间资源等。

构建最优化模型一般包括决策变量、约束条件、目标函数三个要素。决策变量是指最优化决策中待确定的因素；约束条件是指在进行最优决策时对变量的限制，即资源约束，包括资金约束、技术约束、物质约束、时间约束等；目标函数指最优决策希望要达到的效果，通常用数学函数表达。

二、生产计划的最优决策模型

（一）模型概要

生产计划是经营预算的重要环节，企业进行年度预算的起点是目标利润，根据目标利润进行销售预算，根据销售预算进行生产预算，即“以销定产”。因此，生产计划决策的重点在于根据料、工、费、时等资源约束，以满足需求为前提，决定如何进行生产计划的安排，包括资金配置、产品组合、时间进度等，从而达到利润最大化或成本最小化的目标。

生产计划的决策变量包括生产量、库存量等，关键技术主要是规划求解工具的应用和SUMPRODUCT函数的应用。

（二）问题描述

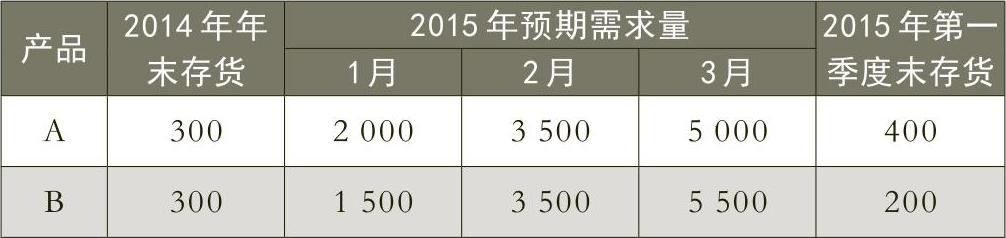
公司主要生产A、B两种机器零件。根据目标利润和市场需求，2015年第一季度的需求量及期初存货量、期末存货量资料见表1，其中，期末存货量为根据第二季度市场需求预测，为了满足销售需求应保有的最低存货量。根据生产技术与单耗的测算，产品生产成本和储存成本资料见表2。根据预测，企业2015年第一季度可用资源如表3。决策问题：在满足需求的情况下，如何安排生产与库存计划，使得总成本最小？该决策的目标函数是成本最小化；约束条件包括产品需求约束、库存约束、资源消耗约束；决策变量为产品生产量和存货量。

（三）建模的技巧与步骤

本文的计算模型见：http://wensubin.ys168.com之文件夹“《财务与会计》论文”之“生产经营最优化决策模型.xlsx”之“生产计划”工作表。

第一步：在数据区输入相关变量及原始数据，见工作表“数据区”表1、表2、表3。

第二步：设计计算分析区。计算分析区包括三个区域：决策变量区、约束条件区（需求约束、库存约束、资源消耗约束）、目标函数区。

特别需要说明的是，目标函数的表达式必须是决策变量的函数，以便运用规划求解工具进行最优化决策。

第三步：运用规划求解工具进行最优化决策。首先加载规划求解工具，依次点击“文件-选项-加载项”，在下方“管理（A）：”处，选择“Excel加载项”，点击“转到”，勾选相关选项，点击“确定”（见下图）。

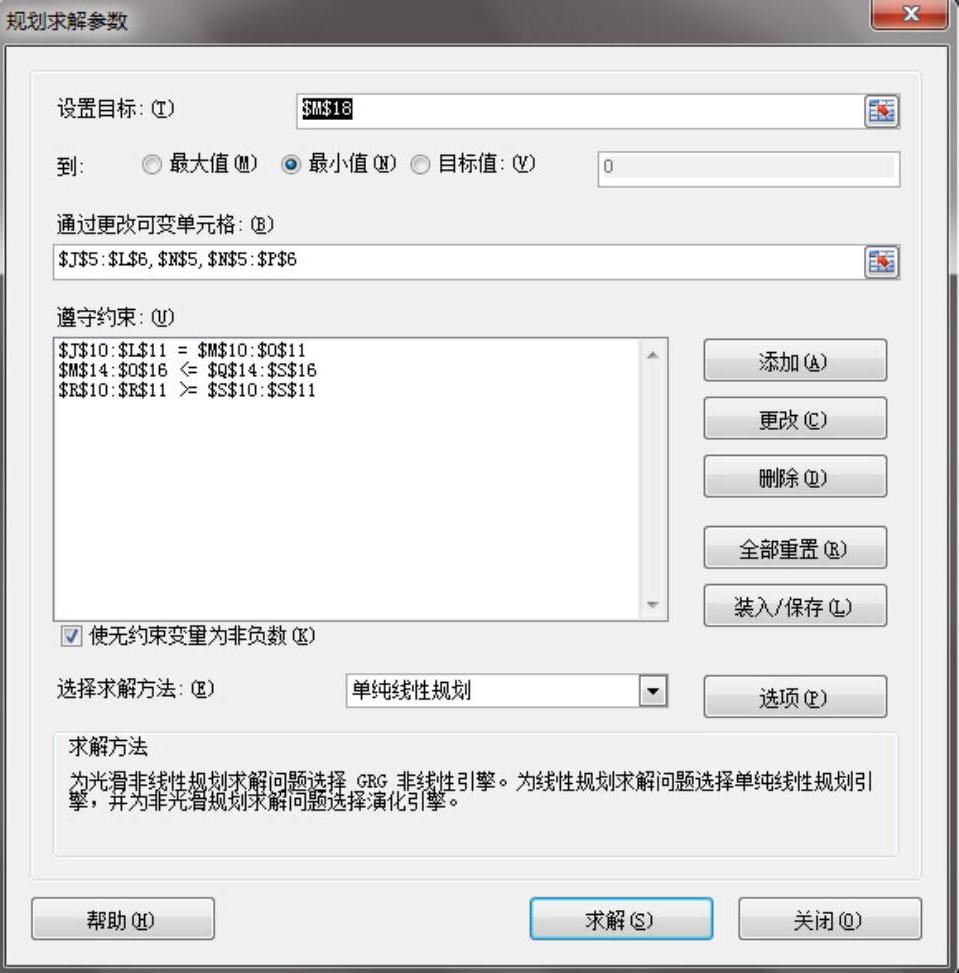
在Excel2010版打开“数据”菜单，点击“规划求解”工具。在“设置目标”处引入目标单元格“$M$18”，在“可变单元格”处引入“$J$5：$L$6,$N$5,$N$5：$P$6”，依次添加约束条件：$J$10：$L$11=$M$10：$O$11、$M$14：$O$16<=$Q$14：$S$16、$R$10：$R$11>=$S$10：$S$11。选择“单纯线性规划”，点击“求解”（见下图）。

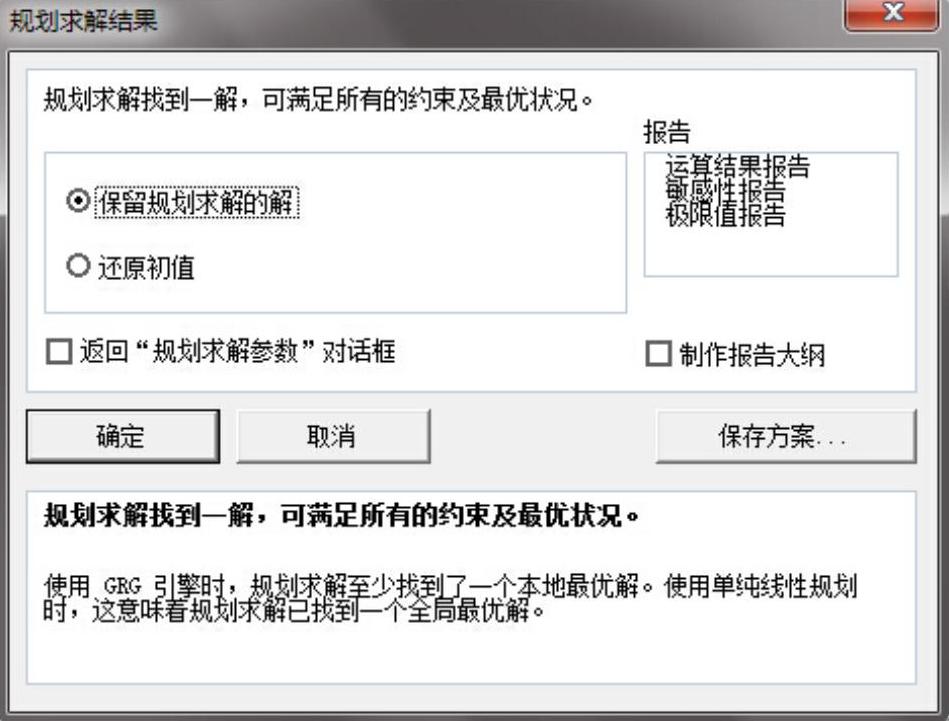
然后，选择“保存规划求解的解”，点击“确定”，得到最优解（见下图）。

因此本案例最优解为：

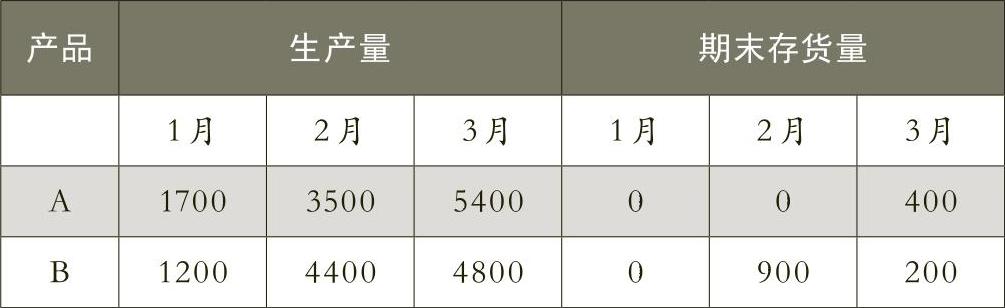
最优成本为632520元。

三、货物配送问题的最优决策模型

（一）模型概要

货物配送问题是物流管理中的重要决策问题，通常需要综合考虑生产能力、配送成本、需求量等多个因素，以合理地安排生产商向销售商的货物运送。配送的决策变量包括生产量、需求量、配送成本等，关键技术主要是规划求解工具的应用。

（二）问题描述

公司有4个生产基地、5个销售配送中心，前者的生产能力分别是1000件、1500件、2000件、800件，后者的需求量分别为1500件、1000件、800件、1100件、900件。从生产基地向销售配送中心的单位运费如下表。决策问题：如何安排配送方案，以达到配送成本最低？

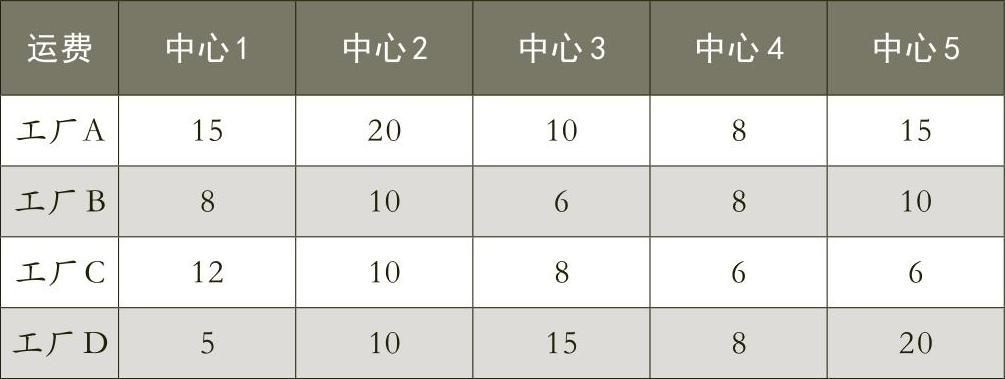
（三）建模的技巧与步骤

本文的计算模型见：http://wensubin.ys168.com之文件夹“《财务与会计》论文”之“生产经营最优化决策模型.xlsx”之“配送问题”工作表。

第一步：在数据区输入相关变量及原始数据，见工作表“数据区”（B2：G6）。

第二步：设计计算分析区。计算分析区包括三个区域：决策变量区、约束条件区（配送量约束、需求量约束）、目标函数区。

首先在区域C10：G13输入决策变量相关信息，即配送量，初始值设为1或其他值。然后，在（H10：I13）、（C14：G15）输入约束条件，即配送量<=生产能力，接收量=需求量。在目标函数区域输入C17=SUMPRODUCT(C3：G6,C10：G13)。

第三步：运用规划求解工具进行最优化决策。在“数据”菜单，点击规划求解工具。在“设置目标”处引入目标单元格“$C$17”，在“可变单元格”处引入“$C$10：$G$13”，依次添加约束条件：$C$14：$G$14=$C$15：$G$15、$H$10：$H$13<=$I$10：$I$13。选择“单纯线性规划”，点击“求解”（图略）。

得到最优解为：（见本页右上图）

最优总运输成本为38400元。

以上问题为一级分销配送问题，如果延伸为多级配送问题，可用同样的方法进行优化。

四、销售网点问题的最优决策模型

（一）模型概要

选择销售网点是企业经营决策的重要内容，尤其是零售业和超市，销售网点过少不利于产品销售，网点过多又会增加销售网点的管理和运营成本。因此，如何合理地分布销售网点是一个重要的决策问题。此类问题可以简化为“是否设置某销售网点”，即“是”或“否”，所以可运用运筹学中的0-1规划进行优化。

（二）问题描述

某超市经过市场调查与细分，将NJ划分为8大消费区域，计划设立4个分销门店，所覆盖的区域分别如下表所示。决策问题：如何设置门店，使门店运营费用最低。

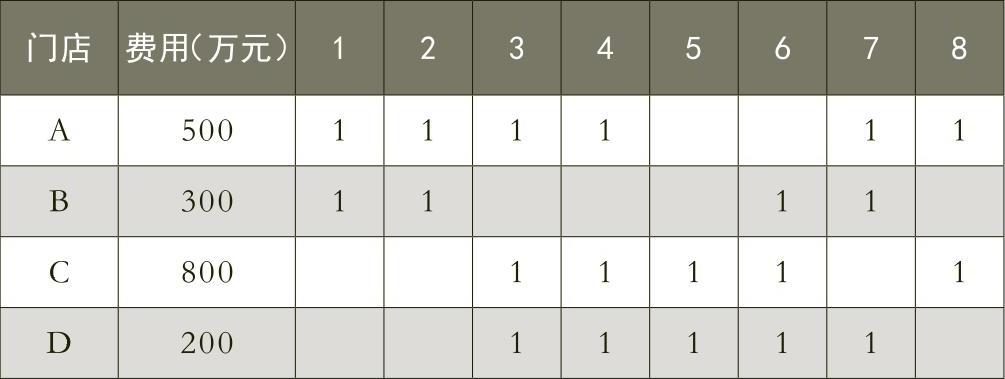
（三）建模的技巧与步骤

本文的计算模型见：http://wensubin.ys168.com之文件夹“《财务与会计》论文”之“生产经营最优化决策模型.xlsx”之“销售网点问题”工作表。

第一步：在数据区输入相关变量及原始数据，见工作表“数据区”（B2：K6）。

第二步：设计计算分析区。计算分析区包括三个区域：决策变量区、约束条件区、目标函数区（公式略）。

第三步：运用规划求解工具进行最优化决策。

经最优化决策可得：应设置A、D两个网点。最优成本为700万元。■

（本文受国家自然科学基金资助项目<71372008>、教育部人文社会科学研究一般项目<10YJA630164>、江苏省高校哲学社会科学研究项目<2011SJD630017>的资助，本文作者温素彬系全国会计领军<后备>人才学术类二期学员）

责任编辑 李卓