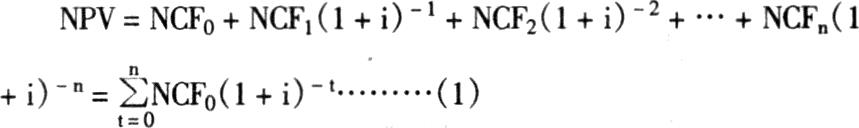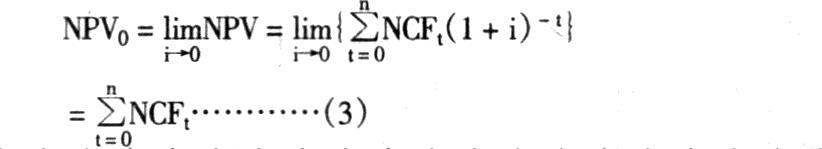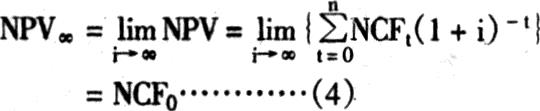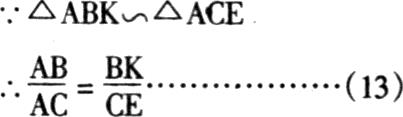摘要:
《财务与会计》1996年第2期和第4期分别刊登了周其亚同志的《内含报酬率新解法——几何法》(以下简称《几何法》)和于慧源、朱启莲同志的《求内部收益率的“外插法”》(以下简称《外插法》)两篇文章,分别就改进现行内插法的问题提出了设想。他们的观点虽然具有一定的实用价值,但均未从理论上严密论证,颇感言犹未尽。本文试图从数学推理中论证,内插法、几何法、外插法的实质都是比例法,计算结果都不可能绝对精确,因为比例法是用直线来代替曲线的。
为了论述的方便,特将本文所使用的数学符号定义如下:
NPV—净现值;NCFt——第t期的现金净流量;i—利息率、折现率;IRR—内含报酬率;n——项目有效期。
一、净现值曲线的数学描述
内含报酬率的计算与净现值的计算密不可分,要想科学地分析内含报酬率的求解方法就必须对净现值与折现率之间的依存关系作出正确的描述。根据净现值的定义,有如下关系式成立:
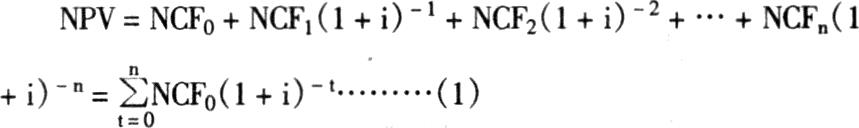
如果把i视作自变量,NPV视作因变量,则(1)式可以抽象地表达为如下的函数关系式:
NPV=f(i)…………(2...
《财务与会计》1996年第2期和第4期分别刊登了周其亚同志的《内含报酬率新解法——几何法》(以下简称《几何法》)和于慧源、朱启莲同志的《求内部收益率的“外插法”》(以下简称《外插法》)两篇文章,分别就改进现行内插法的问题提出了设想。他们的观点虽然具有一定的实用价值,但均未从理论上严密论证,颇感言犹未尽。本文试图从数学推理中论证,内插法、几何法、外插法的实质都是比例法,计算结果都不可能绝对精确,因为比例法是用直线来代替曲线的。
为了论述的方便,特将本文所使用的数学符号定义如下:
NPV—净现值;NCFt——第t期的现金净流量;i—利息率、折现率;IRR—内含报酬率;n——项目有效期。
一、净现值曲线的数学描述
内含报酬率的计算与净现值的计算密不可分,要想科学地分析内含报酬率的求解方法就必须对净现值与折现率之间的依存关系作出正确的描述。根据净现值的定义,有如下关系式成立:
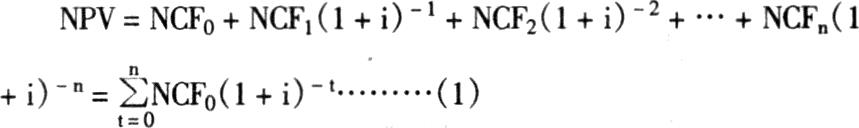
如果把i视作自变量,NPV视作因变量,则(1)式可以抽象地表达为如下的函数关系式:
NPV=f(i)…………(2)
为了合理地描出净现值曲线,下面讨论关于i变动的两种特殊情形:
①当i趋于零时:
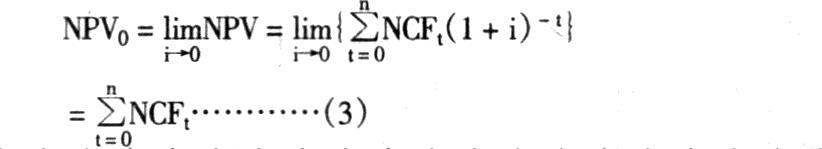
就常规投资项目而言,NPV0>0。因为,如果NPV0≤0,投资项目肯定毫无投资价值。
②当i趋于无穷大时:
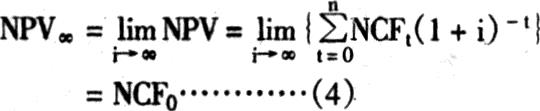
就是说,净现值曲线以NPV=NCF0为水平渐近线。
根据上面的讨论,不难将常规投资项目的净现值曲线描绘成如下的形式:

(图一)
有必要特别指出,净现值与折现率(i)之间的关系间是曲线关系,不是直线关系。
二、内含报酬率的真值与近似值
根据内含报酬率的定义可知,内含报酬率就是使得净现值等于零的折现率。从图一中可知,净现值曲线与横轴相交时,NPV=0,此时的i值即为内含报酬率(IRR)。这就是内含报酬率的真值。
虽然我们能够从理论上指出内含报酬率的真值所在,但要准确地确定它却非易事。
既然内含报酬率的真值不易求得,能否求出它的近似值呢?回答是肯定的。因为在自变量很小的变动范围内,曲线可以用直线近似地替代。这样,在一个合理的范围内,若用直线来取代净现值曲线,就很容易求出内含报酬率的近似值。“以直代曲”的直观描述见图二:

在图二中,B点的i值为IRR的真值。当用直线AC取代弧线ABC后,求出的内含报酬率却是D点的i值,即内含报酬率的近似值。
三、求解内含报酬率近似值的基本方法——比例法
首先必须指出,现在利用各种方法求出的内含报酬率均是其近似值,而不是其值。而所有的方法(包括被广泛使用的内插法及前文述及的几何法和外插法),实质上都是比例法。下面通过一个实例分别讨论各种方法的计算过程。
〔例〕某一投资项目的原始投资为130万元,建设期为0。项目有效经营期为10年,每年的现金净流量为20万元。则NCF0=-130万元,NCF1~10=20万元,n=10年。则该投资项目在不同折现率条件下的净现值如下表所示:

(一)内插法——“以直代曲”的比例法
在上例中,按照通常使用的内插法,最好用8%和9%插值求解。则:

内插法的这一计算过程可用图三直观表示:
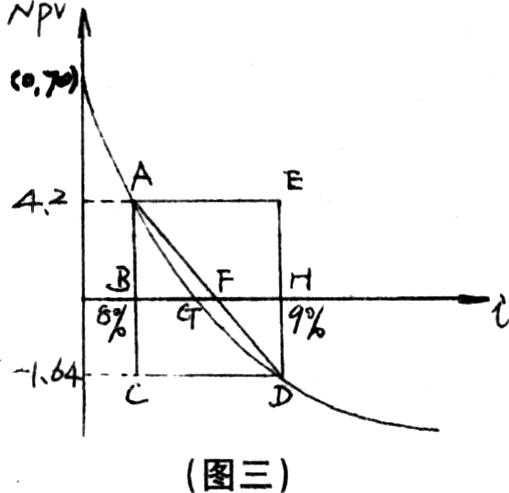
图三中,G点的i值为IRR的真值,F点的i值为IRR的一个近似值(IRR)。很显然,使用内插法求出的IRR值一定大于它的真值。

(8)式与(6)式是完全一致的。可见,内插法是一种典型的比例法。《几何法》一文所介绍的“几何法”的道理就在这里。换言之,几何法仅仅是内插法的一种描述,并不是一种独立的计算方法。
内插法是否只有上述这样一种解法呢?回答是否定的。由图三可知,△ADE~△FDH,△ABF~△FDH,故有:

利用(10)式或者(12)式亦可求出IRR。而且,从理论上分析,三种公式((8)式、(10)式和(12)式)所求出的结果应绝对一致。但在实际运算中,计算结果可能会受到不能整除的小数的影响而使计算结果之间有微小的差别。
可见,即使内插法也不象现行教科书中介绍的那样只有一种求解方法。
以上的计算是用8%和9%插值进行的。其实,也可以用其他i值插值求得近似的内含报酬率,如8%和10%、7%和9%等等。当然,用不同区间的i值插值,得出的计算结果是不同的,因为它们分别用不同的直线来代替曲线。由此不难发现,内含报酬率的近似值是多值的。
(二)外插法——“以直代曲”的比例法
外插法是与内插法相对而言的,它不是在NPV=0的两边插值求解,而是在NPV>0或NPV<0的一方插值求解内含报酬率。实质上,外插法仍然是一种建立在“以直代曲”假设基础上的比例法,这一点从图四中可清楚地看出。
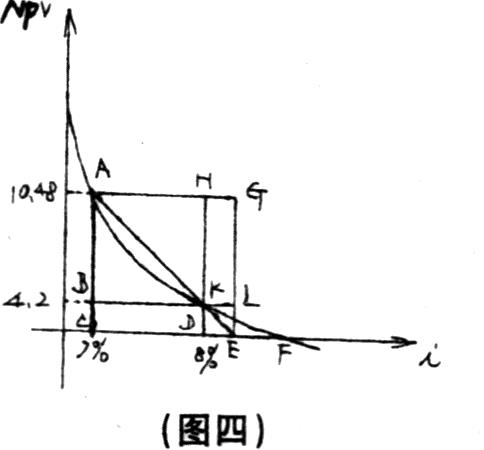
在图四中,F点是内含报酬率的真值,E点则是它的近似值。可见,使用外插法求出的IRR值一定小于它的真值。
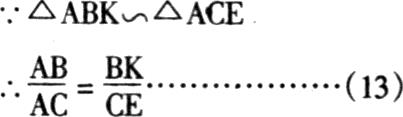

当然,根据图四还可有其他的求解方法。但计算结果从理论上讲应是一致好。
同样的道理,我们亦可用6%和8%或者6%和7%、9%和10%以及9%和11%等不同的i区间值插值求解内含报酬率的近似值,但计算结果必定有所不同。
应该指出,《外插法》一文所举例题计算有误,影响了对这种方法的正确理解。(12%、5年期的现值系数误为0.576,应是0.567,于是,利率为12%时的NPV不是68,而应是-2;文中所列表格最后一栏的第二个数误为3337,应是3333,于是,利率为14%时的NPV不是-792,而应是-796)。
四、几个主要的结论
1.内含报酬率的各种解法都是建立在“以直代曲”基础之上的,因而所求的内含报酬率只能是其近似值。
2.内插法、几何法、外插法的实质都是比例法。
3.用内插法求出的IRR近似值一定大于IRR的真值,而用外插法求出的IRR近似值则一定小于IRR的真值。
4.为了提高IRR计算的精确性,应尽量缩小插值区间。
责任编辑 温彦君

 京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号 京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号