现代生产技术日新月异地发展，给会计理论和方法带来了巨大冲击。尽管诸如计算机集成制造（CIM）之类的现代生产技术能够通过提高生产率，减少废品、返工和缩短生产周期来促进企业的发展，但是，利用投资回收期、投资收益率（ROI）、净现值（NPV）、内部收益率（IRR）和现金流量预测等传统分析方法来证明这些投资的合理性，却是相当困难的。在美国，一些公司因为现金流量分析不能证明技术投资的合理性而放弃生产自动化的选择，并随后由于使用了无效的决策方法而遭受损失的事例屡见不鲜。

传统分析方法得以实施的前提是，投资利益必须可以进行数学计量，如节约额、盈利额、缩短生产周期或扩大销售数量。然而，许多“CIM”投资的利益是“软指标”，不能转换成“硬数据”。因此，面对先进的生产技术，复杂的生产环境和激烈的市场竞争，传统方法日益显露出其本身固有的缺陷，表现在如下几个方面：

1.传统方法必须预测将来的现金流量，但是长期投资的现金流量是不可能准确预测的。事实上，很少有公司会进行工程的后续审计以检验原先预测的准确性，即使少数公司这样做了，其结果往往也是徒劳的。因为一项投资结果通常和其他事项交织在一起，使评价原始预测变得非常艰难。

2.由于某些技术投资结果是“软式”因素，例如不能用数量表示的产品质量和生产灵活性的改进，因此传统方法将这些因素排除在评估范围之外。

3.传统技术根据“现状”来计量预期投资的结果，但实际上，当工业引进新技术之后，所谓“现状”只能维持短暂的瞬间。在大多数情况下，一家公司如果不采用新技术，就会成为竞技场上的失败者，将采用新技术和没有采用新技术的公司作一比较就可以清楚地看到这一点。

4.由于一些分析人员为了支持自己的结论而对难以量化的将来预测结果随意“加工”，因此传统方法仅仅只是一种徒具其表的形式。

当一家又一家公司所拥有的国内市场在国外竞争者咄咄逼人的攻势下逐渐萎缩的时候，美国工业不得不认真考虑生产自动化问题。在这种情况下，美国生产者对传统投资合理性证明技术进行了反思，并尝试新方法。下面简要介绍一下分析CIM和其他技术投资的四种新方法，它们与传统方法有很大的不同，但更适合战略决策的需要。

多重决策模型（MADM）

采用多重决策模型评价技术投资的时候，必须考虑能用数量表示的财务和非财务因素以及不能用数量表示的因素。

MADM程序如下：

首先，分析者将影响投资结果判断的重要因素列成一份名单。例如，假设分析者在评估投资时经常使用净现值法或回收期法，那么这些方法就必须包括在名单之内。此外，名单还包括生产复杂性降低等能用数量表示的非财务因素以及设计灵活性和公司形象等不能用数量表示的因素。

其次，分析人员对每一因数都赋一个值，或称为权数，代表它对公司的重要性，权数的总和等于100。（见表1）

再次，分析人员对公司每一可能的行动方案根据其效果好坏评定等级。对象设计灵活性这样的复杂因素，等级评定却非常简单：0表示预期灵活性降低；1表示预期灵活性不受影响；2表示预期灵活性有所改进。这样，继续维持现有技术的决策设计灵活性等级为1，而CIM投资决策设计灵活性等级为2。

对可以用数量表示的财务因素如NPV来说，等级标度可以改进得更具体一些。例如：

在更复杂的情况下，等级标度将超出0—2。

第四，如果需要的话，可以考虑每种选择等级确定的置信度。例如，假设可以确切肯定维持原有技术对设计灵活性不会带来任何影响，那么其设计灵活性等级的置信度就为1；假设CIM有90%的可能会改进设计灵活性；那么其设计灵活性等级的置信度就为0.9。

最后，计算出每种选择的得分，它等于各种因素权数乘以评定的等级再乘以等级置信度的总和。

在表1中，采用新技术的得分超过维持现有技术的得分（126＞118），表明采用新技术的决策是可行的。

分层分析过程（AHP）

分层分析过程和MADM基本相似，但比MADM更精确、更全面。

AHP要求保持因数权数确定的一致性和准确性。例如，如果减少缺陷的重要性被认为两倍于缩短客户响应时间，而缩短客户响应时间的重要性又三倍于提高设计灵活性，那么减少缺陷相对于提高设计灵活性来说，前者的重要性就六倍于后者。

研究和开发方法（THE R&D APPROACH）

这种方法不把新技术投资看成是资本投资，而是看成一项研究和开发工程。第一步，评估技术投资的预期利益。如果其利益非常具有吸引力，就接着开始第二步，决定是否存在将工程总成本控制在预期利益之下的途径。

进行上述评估有两种方法：全公司统一法和多功能法。按照多功能方法，生产一种产品的所有活动都被自动化，如果效果很好，第二步就是估计将生产所有产品的所有活动全部自动化所需的成本，并且找到一种降低成本的方法。

不确定性方法（UNCERTALNTY APPROACH-ES）

不确定性是指分析人员不能准确估计一项工程成功或失败的可能性。处理不确定性有许多决策方法，其中之一称之为赫维茨原理（Hurwicz s principle）。

有了适当确定的悲观——保守和乐观——冒险复合的组合，代表一项投资不成功或成功的可能性，赫维茨原理可以在高度不确定性条件下作出优化选择。这个组合的确定是一个较为复杂的问题，一开始，决策层中不同的成员可能有不同的观点。但是，经过专家试验多次，最终决策层中大多数或所有成员的认识可以达成一致。

以上四种方法各有不同的特征，它们之间若干异同点的比较列示在表3中。

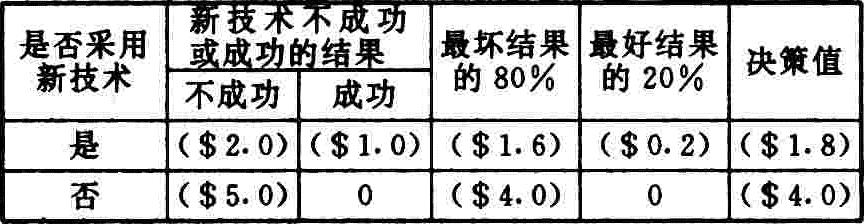
为了应用赫维茨原理，分析人员必须先打一个底稿，如表2所示。在表中，行和列表示一家资产总额为500万美元而技术投资成本为200万美元的公司可作出的决策选择及其可能的结果。表中前三列表示分析人员的期望值。

下一步，分析人员选择一个悲观——保守或乐观——冒险复合的组合，在表中分别为80%和20%。

然后，分析人员完成底稿的下二列，一列是每一行最坏结果的80%，一列是每一行最好结果的20%。最后一列是前两列之和，由于180万美元的亏损毕竟比400万美元的亏损要好得多，所以这一列就为决策人员回答了“是”或“否”的问题。