 当前位置:首页 > 用户服务 > 过刊查询 > 财务与会计过刊查询 > 《财务与会计》1991年第01期 > 财务与会计1991年第01期文章 > 正文
当前位置:首页 > 用户服务 > 过刊查询 > 财务与会计过刊查询 > 《财务与会计》1991年第01期 > 财务与会计1991年第01期文章 > 正文“正弦函数法”是计算承包企业奖金额的好办法
时间:2020-05-27 作者:王利群 曹伟
[大]
[中]
[小]
摘要:
当前,在经济承包工作中,大都采用较直观、简单的正比例法计算奖金。这种方法的缺陷是:(一)甲乙双方在确定承包利润基数时讨价还价,争论不休。(二)由于起点低,效益猛增,奖金过高不能兑现,年末只好硬性将承包利润基数提高;或者由于人均奖金过低,不得不给予适当照顾,结果使政策缺乏严肃性。为解决这些问题,笔者认为采用“正弦函数法”来计算奖金提取额不失为一个好办法。
一、正弦函数法的基本内容
正弦函数法又称曲线法,是根据正弦函数的性质,在实际工作中,规定sin△L≤15048之间的正弦值)来计算出利润的增长幅度,从而计算应提奖金额的一种方法。正弦函数法计算奖金额用图象表示如下:(见图1.1)
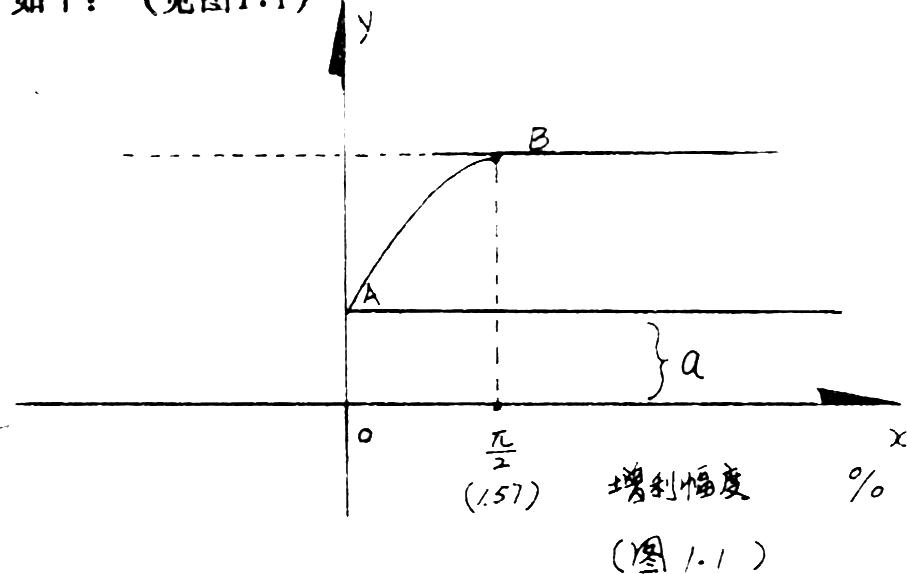
图中a表示完成基数利润所得的基本奖金,AB点表示超额利润所提取的超额奖金。
目前,一般采取的奖金计算方法是直线法,也就是正比例法,是根据公式y=a+bx来求得的。直线法计算奖金额的公式是:
应得奖金额=基本奖+超额利润×提奖比例
其图象如下:(见图1.2)
当前,在经济承包工作中,大都采用较直观、简单的正比例法计算奖金。这种方法的缺陷是:(一)甲乙双方在确定承包利润基数时讨价还价,争论不休。(二)由于起点低,效益猛增,奖金过高不能兑现,年末只好硬性将承包利润基数提高;或者由于人均奖金过低,不得不给予适当照顾,结果使政策缺乏严肃性。为解决这些问题,笔者认为采用“正弦函数法”来计算奖金提取额不失为一个好办法。
一、正弦函数法的基本内容
正弦函数法又称曲线法,是根据正弦函数的性质,在实际工作中,规定sin△L≤15048之间的正弦值)来计算出利润的增长幅度,从而计算应提奖金额的一种方法。正弦函数法计算奖金额用图象表示如下:(见图1.1)

图中a表示完成基数利润所得的基本奖金,AB点表示超额利润所提取的超额奖金。
目前,一般采取的奖金计算方法是直线法,也就是正比例法,是根据公式y=a+bx来求得的。直线法计算奖金额的公式是:
应得奖金额=基本奖+超额利润×提奖比例
其图象如下:(见图1.2)
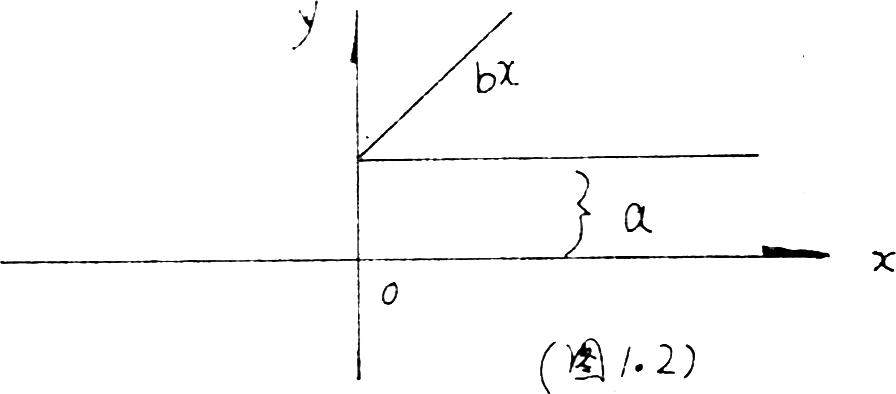
图中a表示基本奖,bx表示超额利润所提取的超额奖金。
我们把上述直线法的公式变化一下,可得下面公式:
应得奖金额=基本奖+基数利润×增利幅度×提奖比例
为叙述方便,可i设:
y=应提奖金额
a=基本奖
b=基数利润
△L=增利幅度(用百分数表示)
c=提奖比例
这时,原公式可以简单地记作:
y=a+b·△L·c
正弦函数的公式就是在上式的基础上,取△L(增利幅度)的正弦函数值。即:
y=a+b·sin△L·c
在实际工作中,我们可以规定sin△L≤1(取0~π/2之间的正弦值)。△L在数学中代表弧度。经查数学用表可知,1弧度=57°17′45″=57.296°。π=3.14,π/2=3.14/2=1.57。那么,我们取当增利幅度为基数利润的157%时,也就是说,当△L=1.57时,sin△L=sin1.57=1为极大值,这时提取的奖金额为最高数额。
二、举例说明“正弦函数法”的运用及优点
例1:某承包部门承包的基数利润是15万元,完成基数利润,可得基本奖金2万元。超额完成,则超额部分按10%提取奖金额。
我们设该部门实际完成利润情况如下:

(一)采用直线法所计算的应提奖金额
按公式:y=a+bx
(1)当增利额为4.5万元时,a=2,b=4.5,x=10%,所以
y=a+bx
=2+4.5×10%
=2.45(万元)
(2)当增利额为6万元时,
y=2+6×10%=2.6(万元)
(3)当增利额为10万元时,
y=2+10×10%=3(万元)
(4)当增利额为20万元时,
y=2+20×10%=4(万元)
(5)当增利额为25万元时,
y=2+25×10%=4.5(万元)
(二)采用正弦函数法计算的应提奖金额
按公式:y=a+b·sin△L·c
(1)当增利额为4.5万元时,增利幅度是30%,即0.3。这时,a=2,b=15,△L=0.3,c=0.1,应提奖金额为:
y=a+b·sin△L·c
=2+15×sin0.3×0.1
=2.443(万元)
(注:sin△L的求法:当增利幅度△L=0.3时,sin△L=sin0.3,这时0.3指的是弧度,已知1弧度=57.296°,那么0.3弧度=0.3×57.296°=17.1888°,它的正弦函数值用计算器按sin键后可得0.2955。其它sin△L的求法类同)。
(2)当增利额为6万元,增利幅度是40%,即0.4时,应提奖金额为:
y=2+15×sin0.4×0.1
=2.584(万元)
(3)当增利额为10万元,增利幅度是67%,即0.67时,应提奖金额为:
y=2+15×sin0.67×0.1
=2.931(万元)
(4)当增利额为20万元,增利幅度是130%,即1.3时,应提奖金额为:
y=2+15×sin1.3×0.1
=3.445(万元)
(5)当增利额为25万元,增利幅度是166%,即1.66时,由于正弦函数法取(0~π/2之间的正弦函数值,所以,sin△L=sin1.66=sin1.57=1。这时,应提奖金额为:
y=2+15×sin1.57×0.1
=3.5(万元)
用两种方法计算的奖金额对照如下:
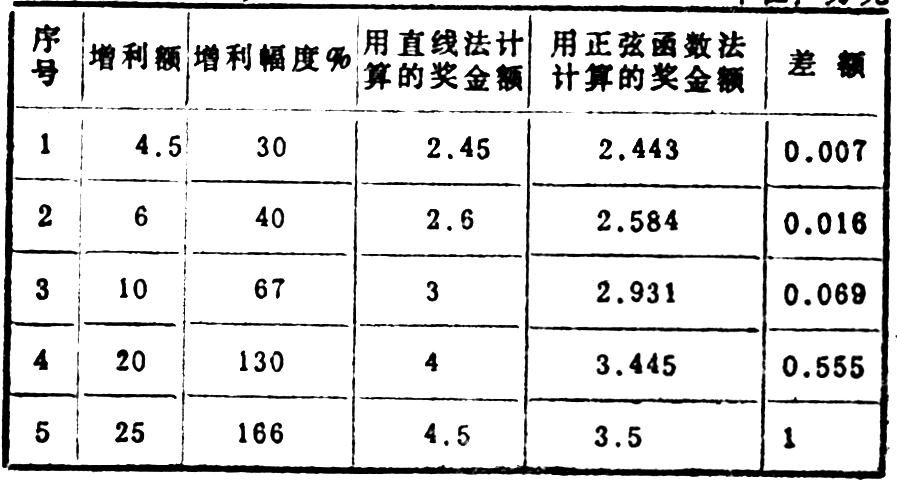
例2:某承包部门根据上年实际,年初承包基数利润10万元,完成基数利润可得基本奖1.2万元,超额利润部分则按10%提奖。结果该部门年终实际完成利润25万元,超额完成15万元,该部门应得奖金:
根据公式:y=a+b·sin△L·c由题可知:a==1.2,b=10,c=0.1,△L=5250
×100%=150%=1.5
计算:y=1.2+10×sin1.5×0.1
=2.198(万元)如果该部门年初把基数利润硬是由10万元压到8万元,那么,增利幅度△L=5250×100%=212.5%=2.125。根据公式的约束条件,当△L>1.57时,当以1.57计。所以,该部门应得奖金额是:
y=1.2+8×sin1.57×0.1
=2(万元)
如果该部门年初能根据自己的实际水平,主动把利润基数提到12万元,那么,该部门应得的奖金额是:增利幅度△L=5250×100%=108%=1.08
y=1.2+12×sin1.08×0.1
=2.258(万元)
由此可见,完成同样的利润额,把基数利润提高后,所提取的奖金不但不会减少,反而有所增加,从而促使承包者根据实际情况主动提高利润基数。反之,将基数利润压低后,按正弦函数法计算应得的奖金额反而降低了,从而可以避免现行计奖方法在利润基数上争论不休的问题。同时,它还能避免承包部门由于起点低、潜力大,或因外部因素而造成的奖金猛增,从而有利于奖金的宏观控制。
另外,正弦函数法与直线法提取的奖金额在增利幅度低幅度上升时基本接近。如增利幅度在30%以下时,两种方法提取的奖金额基本相同(请参考表1-2)。只有当增利幅度在30%以上时,即增利幅度在0.3<△L≤1.57时,提取的奖金额才呈递减趋势。这正好解决了由于效益猛增,奖金无法全部兑现的矛盾。
三、为鼓励承包部门创造更好的经济效益,我们还可以在上述基础上再增一些内容。
①为鼓励上年经济效益好、对单位贡献较大的部门,可以在研究下一年的提奖中增加一定的系数以资鼓励。例如,我们设这部分为E,且要求1 y=a+E·b·sin△L·c ②为避免增利幅度达到157%后,影响承包部门再创经济效益的积极性,还可增设产值增长率系数,设这部分指标为D,且要求1 y=a+E·D·b·sin△L·c 例3:某车间素质较好,上年经济效益高,对全厂利润指标完成贡献较大。因此,此项加奖系数为1.1。今年承包基数利润15万元,实际完成19.5万元,而且,产值增长20%,此项加奖系数为1.1。按合同规定,完成基数利润可得基本奖1.2万元。超额利润部分按10%提奖。 那么,该车间今年应得奖金额是:根据公式:y=a+E·D·b·sin△L·C由题可知:E=1.1,D=1.1,b=15,△1=5250=0.3c=0.1,a=1.2计算:y=1.2+1.1×1.1×15×sin0.3×0.1 =1.74(万元) 如果按现行办法计算,因为上年的贡献不考虑,产值增长率也不考虑。则该车间应计提奖金: y=a+bx =1.2+4.5×10% =1.65(万元) 与正弦函数法相比,少提了1.74-1.65=0.09万元。由此可见,现行计奖办法没能起到鼓励先进的作用,而正弦函数法把上年水平作为本年提奖额的一个因素进行考虑,而且随本年实际浮动,这就起到了鼓励先进更上一层楼的作用。 总之,正弦函数法优于现行的直线法,但这并非说它就是完美无缺的方法,它也有不完善的地方。随着经济承包工作的深入开展,愿大家共同来认识和探讨这一方法,使其更完善,更好为搞好经济承包工作服务。
 附件下载:
附件下载:相关推荐
主办单位:中国财政杂志社
地址:中国北京海淀区万寿路西街甲11号院3号楼 邮编:100036 互联网新闻信息服务许可证:10120240014 投诉举报电话:010-88227120
京ICP备19047955号 京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
投约稿系统升级改造公告
各位用户:
为带给您更好使用体验,近期我们将对投约稿系统进行整体升级改造,在此期间投约稿系统暂停访问,您可直接投至编辑部如下邮箱。
中国财政:csf187@263.net,联系电话:010-88227058
财务与会计:cwykj187@126.com,联系电话:010-88227071
财务研究:cwyj187@126.com,联系电话:010-88227072
技术服务电话:010-88227120
给您造成的不便敬请谅解。
中国财政杂志社
2023年11月
- 主办单位:中国财政杂志社
- 地址:中国北京海淀区万寿路西街甲11号院3号楼
- 投诉举报电话:010-88227120
- 邮编:100036
 京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号





