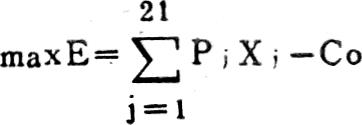摘要:

《财务与会计》1989年第9期刊发的赵明、阎勇两同志的“如何利用线性规划原理确定产品有效产量”一文（以下简称赵、阎文），针对在有限原材料的条件下，如何合理确定产品的品种、产量，以使利润最大化，用意颇佳，对解决企业经营管理中的实际问题有一定的帮助。但该文也有一些疏漏之处，现就主要问题，提出一点商榷意见。

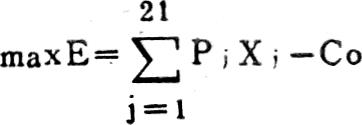
来看，基于产量（Xi）不取负值，要使总利润（E）最大，个别负贡献利润的产品产量，也必须取零。这是总利润最大化的必要条件。根据实际计算，所得结果亦是如此.

2.赵、阎文所举数字实例，用线性规划上计算机运算，似乎不是很适宜。

该文数学模型，主要宜用于交叉型实例——即既有一种产品需用几种原料，又有一种原料供应几种产品，且相互交叉的实例。而且，只有在产品、原料均多于三种的情况下，才宜于编定程序，上计算机运算。但对该文所举实例是一种不常见的非交叉型实例——21种产品一般均各需一种原料，仅有2种原料供应几种产品且均不交叉。笔者认为，在这种情况下，采用推理四则运算要简便得多。

《财务与会计》1989年第9期刊发的赵明、阎勇两同志的“如何利用线性规划原理确定产品有效产量”一文（以下简称赵、阎文），针对在有限原材料的条件下，如何合理确定产品的品种、产量，以使利润最大化，用意颇佳，对解决企业经营管理中的实际问题有一定的帮助。但该文也有一些疏漏之处，现就主要问题，提出一点商榷意见。

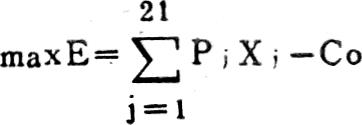
来看，基于产量（Xi）不取负值，要使总利润（E）最大，个别负贡献利润的产品产量，也必须取零。这是总利润最大化的必要条件。根据实际计算，所得结果亦是如此.

2.赵、阎文所举数字实例，用线性规划上计算机运算，似乎不是很适宜。

该文数学模型，主要宜用于交叉型实例——即既有一种产品需用几种原料，又有一种原料供应几种产品，且相互交叉的实例。而且，只有在产品、原料均多于三种的情况下，才宜于编定程序，上计算机运算。但对该文所举实例是一种不常见的非交叉型实例——21种产品一般均各需一种原料，仅有2种原料供应几种产品且均不交叉。笔者认为，在这种情况下，采用推理四则运算要简便得多。