（10n-1）除查错法〔当n=1，2，3时〕，是用10n-1的值即9，或99，或999来除误差额，求出商数并据以判断，进行查找错帐的一种方法。本文仅就数字颠倒和移位等常见错帐进行剖析，介绍这一方法的形成和运用，并找出一些规律性的东西①。

（一）在邻位数颠倒的情况下，误差额=9×A×10n

第一、如e.c误写成c.e、属于角，元位上颠倒。e由元位上退至角位上，c由角位上进到元位上。其误差额为：

e.c-c.e=（e+0.1×c）-（c+0.1×e）

=0.9×e-0.9×c=0.9×（e-c）

=9×（e-c）×10-1………………第一式②

在第一式中（e-c）就是位置互换的邻位数之差。

第二、如ab误写成ba，属于元、十位上颠倒。a由十位上退至元位上；b则由元位上进到十位上。其误差额为：

ab-ba=（a×10+b）-（b×10+a）

=9×a-9×b=9×（a-b）

=9×（a-b）×100…………………第二式

在第二式中（a-b）仍是位置互换的邻位数之差。

第三、如cde误写成dce，属于十、百位上颠倒.c由百位上退至十位上；d则由十位上进到百位上。其误差额为：

cde-dce=（c×100+d×10+e）-（d×100+c×10+e）

=90×（c-d）

=9×（c-d）×101…………………第三式

在第三式中（c-d）又是位置互换的邻位数之差！

第四、如abcd误写成bacd，属于百、千位上颠倒。a由千位上退至百位上，而b则由百位上进到千位上。其误差额为：

abcd-bacd=（a×1000+b×100+c×10×d）

-（b×1000+a×100+c×10+d）

=900×a-900×b=900×（a-b）

=9×（a-b）×102………………第四式

在第四式中（a-b）还是位置互换的邻位数之差！！

我们把颠倒的邻位数之差用A表示（1≤A≤9），由第一至四式可以推导出任意数据的邻位数颠倒后的误差额为：9×A×10n。根据上述分析及其结论，可编出下表：

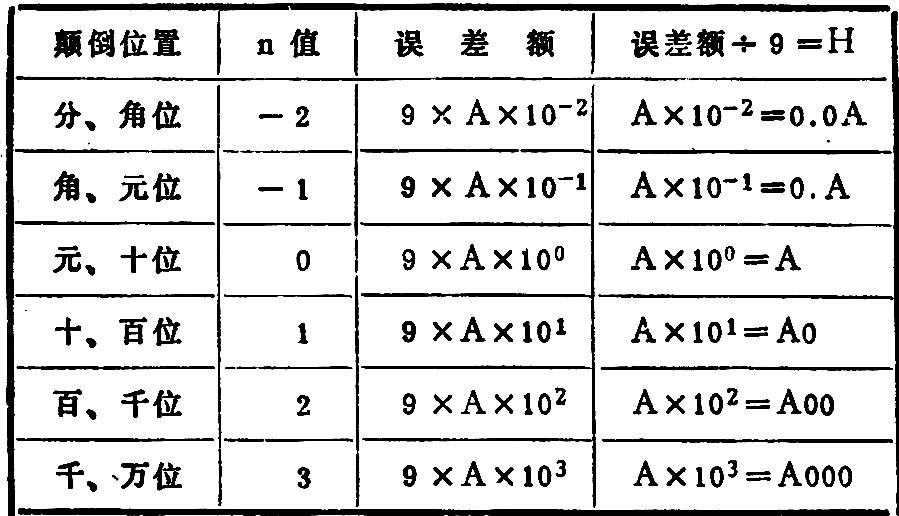
根据表中规律查找邻位数颠倒的差错，就十分方便，现尝试一下：③

例一、已知误差额为720元，求找差错之所在。

〔分析〕H=720÷9=80=8×101，由此得A=8；n=1。因而可判断为十、百位上颠倒，且颠倒的邻位数差为8

即a91c←→a19c

例二、已知误差额为0.54元，求找差错之所在。

〔分析〕H=0.54÷9=0.06=6×10-2由此得A=6n=-2，因而可判断为分、角位上颠倒，且颠倒的邻位数差为8。

即0.71←→0.17；或0.82←→0.28；或0.93←→0.39

（二）在隔位数颠倒的情况下 误差额=99×A×10n

第一、若将be.a误写为ae.b，此属角，十位上颠倒。b由十位上退至角位上，而a则由角位上进到十位上。其误差额为：

be.a-ae.b（b×10+e+a×0.1）

-（a×10+e+b×0.1）

=9.9×（b-a）

=99×（b-a）×10-1………………第一式

在第一式中（b-a）就是颠倒的隔位数之差。

第二、如将abc误写为cba，此属元、百位上颠倒。a由百位上退至元位上，c则由元位上进到百位上、其误差额为：

abc-cba=（a×100+b×10+c）

-（c×100+b×10+a）

=99×（a-c）

=99×（a-c）×100…………………第二式

在第二式中（a-c）又是颠倒的隔位数之差！

第三、若将bacd误写成cabd。此属十、千位上颠倒，b由千位上退至十位上，而c则由十位上进到千位上。其误差额为：

bacd-cabd=（b×1000+a×100+c×10+d）

-（c×1000+ax100+b×10+d）

=990×b-990×c=990×（b-c）

=99×（b-c）×101………………第三式

在第三式中（b-c）仍是颠倒的隔位数之差1！

我们把颠倒的隔位数之差仍用A表示（1≤A≤9），由第一至三式可以推导出任意数据的隔位数颠倒后的误差额为：99×A×10n，根据上述分析及其结论，可编成下表：

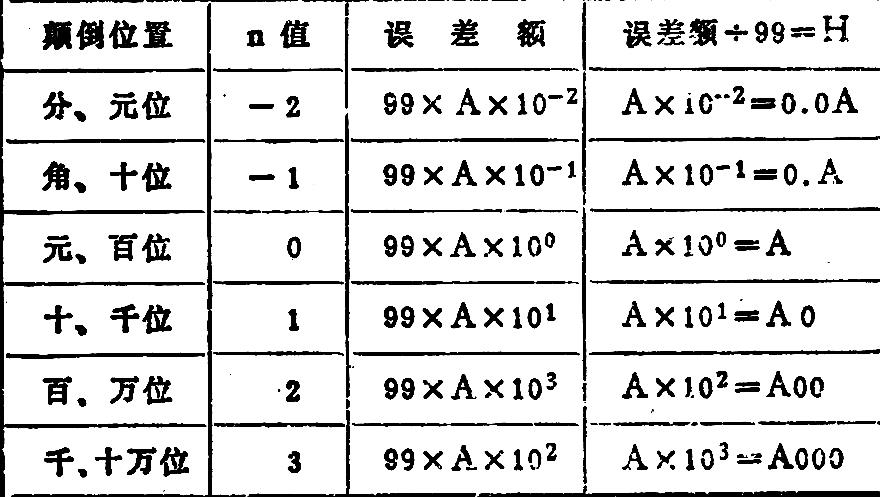
现依上表规律，举例说明隔位数颠倒的差错的查找。

例一、已知误差额为485元，求找差错之故。

〔分析〕H=495÷99=5=5×100由此可见A=5n=0因而判断为元、百位上颠倒，且颠倒的隔位数之差为5。

即bc1←→1cb；762←→267；8e3←→3e8；9d4←→4d9

例二、已知误差额为79200元，求找差错之故。

（分析〕H=79200÷99=800=8×102由此可见A=8，n=2因而可判断为百，万位上颠倒，且颠倒的隔位数之差为8。

即9e1ab←→1e9ab

（三）在数据移位的情况下误差额=（10n-1）×小

因此误差额=大-小=10n×小-小=（10n-1）×小

在上式中n与数据小数点所移位数相同。

第一，当数据移动一位时，n=1其误差额=（101-1）×小=9×小

第二，当数据移动二位时，n=2其误差额=（102-1）×小=99×小

第三，当数据移动三位时，n=3其误差额=（103-1）×小=999×小

数据的小数点移一二位的差错常见，移三位少见，移三位以上几乎不大可能了，因此不必再推导。现据上述分析可编制下表：

依据上表中规律，进行数据移位差错的查找就十分方便。兹举三例：

例一、已知误差额为52494.39元，求找差错之故。

〔分析〕H=52494.39÷9=832.71，刚好整除，可判断为数据移动一位之误，且小=5832.71则大=58327.10即5832.71←→58327.10其大小数之差刚好为52494.39元

例二、已知误差额为778483.53元，求找差错之故

（分析〕H=778483.53÷99=7863.47，刚好整除，可判断为数据移动二位之误，且小=7863.47则大=786347.00即7863.47←→786347.00其大小数之差刚好为778483.35元

例三、已知误差额为9330.66元，求找差错之故

〔分析〕H=9330.66÷999=9.34，刚好整除，可判断为数据移动三位之误且小=9.34则大=9340，00即9.34←→9340.00其大小数之差刚好为9330.66元。

注：

①为表述方便，本文所用英文小写字母a、b、c、d、e等均可代表0～9中任一自然数。

②第一式是根据“76=7×10+6”的道理恒等变形所成。以下各式均同。

③“←→”两箭头所指方向，一个为正确的，一个则是错误的。