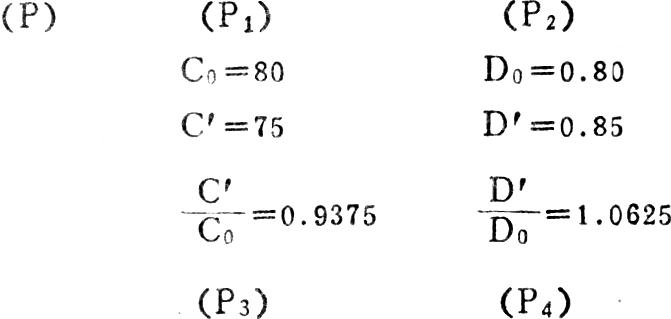摘要:
N0=30×26×0.8×80=49920
N1=25×26×0.8×80=41600 N1-N0=-8320……………△B
N2=25×27×0.8×80=43200 N2-N1=1600……………△A
N5=25×27×0.85×80=45900 N3-N2=2700……………△D
N4=25×27×0.85×75=43031.25 N4-N3=-2868.75……………△C
N4-N0=-6888.75……………△N
再按CDAB的顺序排列结果,得
N0=80×0.8×26×30=49920
N1=75×0.8×26×30=46800 N1-N0=-3120…………△C
N2=75×0.85×26×30=49725 N2-N1=2925…………△D
N3=75×0.85×27×30=51637.50 N3-N2=1912.5…………△A
N4=75×0.85×27×25=43031.25 N4-N3=-8606.25…………△B
N4-N0=-688875…………△N
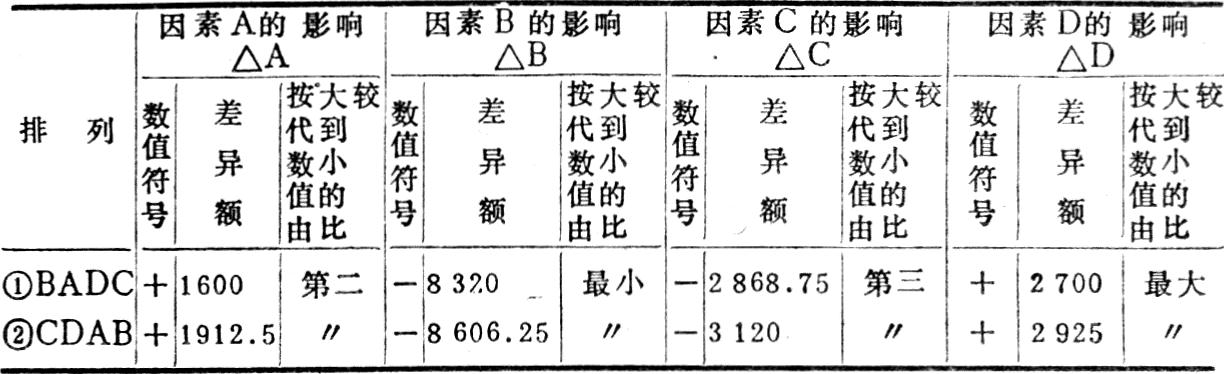
把这两种排列的分析结果,整理归纳如下:
当人们应用连锁置换法进行财务分析时,常为因素排列顺序不同造成差异迭变的问题所困惑,长期以来,普遍认为是因素置换法的先天缺陷。其实,究其原因,并不全是分析技术本身的不足,也有可能是我们对它的内涵认识不够全面深入。本人想就这个问题谈点一孔之见。
一、...
N0=30×26×0.8×80=49920
N1=25×26×0.8×80=41600 N1-N0=-8320……………△B
N2=25×27×0.8×80=43200 N2-N1=1600……………△A
N5=25×27×0.85×80=45900 N3-N2=2700……………△D
N4=25×27×0.85×75=43031.25 N4-N3=-2868.75……………△C
N4-N0=-6888.75……………△N
再按CDAB的顺序排列结果,得
N0=80×0.8×26×30=49920
N1=75×0.8×26×30=46800 N1-N0=-3120…………△C
N2=75×0.85×26×30=49725 N2-N1=2925…………△D
N3=75×0.85×27×30=51637.50 N3-N2=1912.5…………△A
N4=75×0.85×27×25=43031.25 N4-N3=-8606.25…………△B
N4-N0=-688875…………△N
把这两种排列的分析结果,整理归纳如下:

当人们应用连锁置换法进行财务分析时,常为因素排列顺序不同造成差异迭变的问题所困惑,长期以来,普遍认为是因素置换法的先天缺陷。其实,究其原因,并不全是分析技术本身的不足,也有可能是我们对它的内涵认识不够全面深入。本人想就这个问题谈点一孔之见。
一、演例的启示和推理:为便于全面深入地进行探索,引四因素结构的例题分析如下:
设某汽车运输场原计划全月营业26天,日均出车30辆次,单车油耗定额80公斤,计划价每公斤0.80元,实际全月营业27天,日均出车25辆次,实际油耗75公斤,实际油价每公斤0.85元。请用连锁置换法分析该运输场营业天数,出车辆次、单车油耗及汽油单价四因素变动对费用开支的影响程度。
解:令A代表营业天数;B代表出车辆次;
C代表单车油耗;D代表汽油单价。
先按BADC的顺序排列,得:
表列资料说明两种排列的分析结果,虽然同一因素的两个差异额数值各异,但有两点,却是共同的,即:(1)差异额符号的正负方向是相同的;(2)差异额按代数值的大小比较,先后的次序也是相同的。从这关键的启示中我设想,在四因素的全部排列中倘若所有结果都符合附表I所表明的情况,且没有一个例外,就足以证明存在一定的规律,这种规律就是连锁置换法内涵的本质。为此我将A、B、C、D四因素全排列的分析数据作了演算,证实了前面的推理是对的。尽管在全部分析中,同一因素的24个差异额多有不同,但数值的符号却都是同一的;其代数值按大小比较的先后次序也是完全相同的。在所有的分析结果中,因素差异额的绝对值最大的都是因素D(汽油单价的影响),其次是因素A(营业天数的影响),居第三位的是因素C(单车油耗的影响),最后是因素B(出车辆次的影响)。
我用同样的方法进行了五因素差异的分析,结果也符合上述推论。
二、因素差异内涵的根据——因素置换率:前述分析证实在不同的众多排列中,同一因素差异额的数值再三迭变,但诸因素间彼此的相对关系,一直保持恒定,根本依据是诸因素计划量和实际量之间存在着固定的因素置换率,例如在前述四因素的例题中诸因素为:
计划量 A0=26 B0=30
实际量 A′=27 B′=25
因素置换率5452
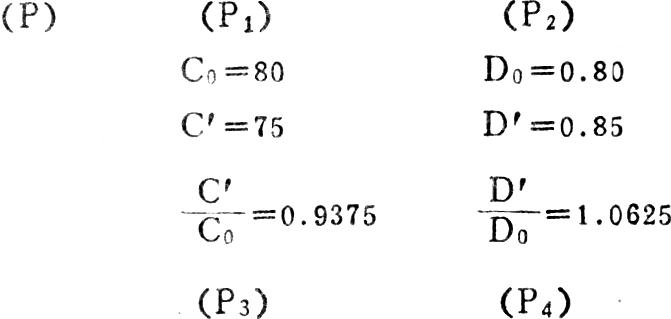
这四种因素置换率按大小比较的关系式是:5452即:P4>P1>P3>P2再看本文所列举的差异额,都是通过N1-N0,N2-N1等置换式运算得来的,因此这些因素差异额完全可以用计划总额(N。)和因素置换率的乘积来直接计算。为证实这一点,现采用计划总额N。的值和诸因素的置换率来计算△D的数值。计算步骤:
1、当因素D所处的相对位置排在首位时。例如“DBAC”则:
△D=N0×(P4-1)
=49920×0.0625=3120
2、当因素D排在第二位时。例如“ADBC、BD AC、CDAB”则:
△D=N0×(P4-1)×P1
=49920×0.0625×1.0384
=3240
以下类推为:
△D=N0×(P4-1)×P2
△D=N0×(P4-1)×P3(计算从略)
3、当因素D排在第三位时。例如“ABDC、A CDB、BCDA”则:
△D=N0×(P4-1)xP1P2
△D=N0×(P4-1)×P1P3
△D=N0×(P4-1)×P2P3(计算从略)
4、当因素D排在最末位时,如“CABD”则:
△D=N0×(P4-1)×P1P2P3(计算从略)
其他如△A、△B、△C的值也可以根据同样的原理和方法来计算求得。
三、结束语:综上归纳可以肯定连锁置换法分析技术所提供的信息内涵不会受因素排列的影响,就是说,任何排列的结果,实质都是同一的,是可以信赖的,它能为我们加强管理,指示确切的位置和方向。所以我们不要机械地直接应用这些分析结果的具体数值,而只应把它们作为基本的参数。
在差异总额已经确定了的前提下,由于排列不同,因素差异额必然会此消彼长,这对连锁置换法来说不过是一种表象的变化,并不涉及信息内涵的本质,财会人员应不为差异额迭变的表象所迷惑,而应抓住它内涵的本质,使之服务于我们的分析工作。
 京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号 京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号