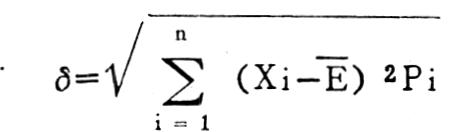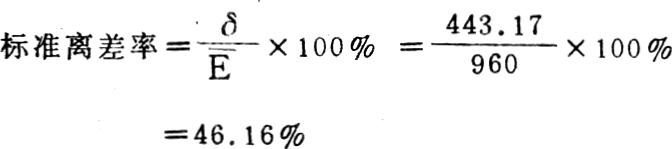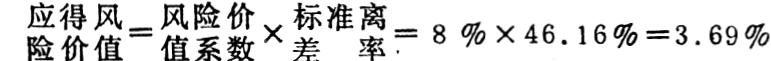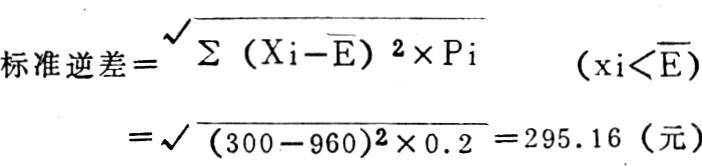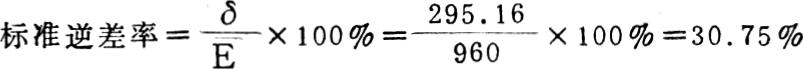读了《财务与会计》1986年第12期登载的张克业同志的《谈谈风险价值原理》一文（以下简称张文）后，很受启发，但同时也感到该文对风险程度和应得风险价值的计算表述有商榷之处。下面谈谈本人的一点肤浅认识。

一、关于风险程度问题。张文认为风险的大小可以用标准离差来反映。用δ代表标准离差，则得计算公式：δ=6462式中：x为随机利润E为利润期望值，Pi为概率。我认为以上表述是不正确的。所谓风险，是指某方案期望目标有达不到的可能。而张文所提标准离差是统计中反映平均数的代表程度的一个指标，它包括了各变量值与平均数的顺差和逆差。所以完全用标准离差代表风险大小是不妥当的。根据风险的含义，张文的公式应再补充一个必要条件，即xi<6462，同时标准离差也应改为标准逆差，这样反映风险大小可相对确切一些。也就是说，只有小于期望目标的随机利润才构成风险。进一步将标准逆差和期望值相比，求出标准逆差率，即表示风险程度，可在不同方案之间比较。用完整的公式表示就是：

式中6表示标准逆差，xi表示小于6462的随机利润，E表示利润期望值，Pi为概率。

二、关于应得风险价值的计算问题。张文根据风险价值是对无风险价值而言的这一关系得出：风险价值=无风险价值×标准离差率。同时又提出投资者根据自己的主观意愿，可以围绕无风险价值，确定一个风险价值系数，于是又得出：风险价值=风险价值系数×标准离差率。我认为以上两个公式的依据是不切实的。从辩证的观点看，风险价值是针对无风险价值而言的，但从经济学的角度看，风险价值只能是针对某一期望目标而言的。因为某一方案的风险价值是对该方案承担了期望目标值难以实现的风险的报酬。所以应得出下列公式：

对于投资者根据自己的主观意愿来确定一个风险价值系数，再计算风险价值，我认为这也是无益的。因为风险价值是投资者的决策依据之一，应尽量做到客观实际地反映。所谓主观意愿只不过是人为地改变这种客观性，这对正确的投资决策是没有帮助的。

总而言之，关于风险程度和应得风险价值问题，张文所述是欠妥的，有时还可能导致错误的决策。我们将张文举例略加变动如下：

投资额10000元，无风险价值6%，风险价值系数8%。

可能出现市场情况： 畅销 一般 较差

风险程度和应得风险价值按张文介绍的方法计算如下：

①计算标准离差δ（即风险大小）

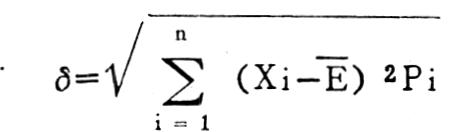
=√(2000-960)²×0.1+(1000-960)²×O.7+(300-960)²×0.2-443.17（元）

②计算标准离差率（即风险程度）

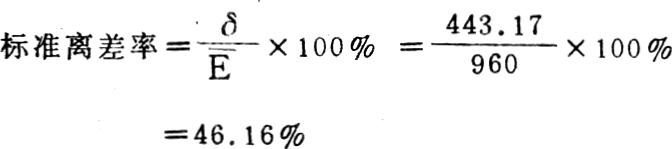
③计算应得风险价值

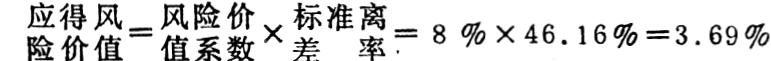
计算结果表明，冒的风险（3.69%）大于风险回收率（3.6%），按投资要求此投资方案是不可取的。但实际上此方案风险并不很大，因为超过期望目标的变量利润概率达到0.8，其余0.2概率的变量利润也占无风险价值50%，这从笔者的计算中可得到证实。按笔者方法计算如下：

①计算标准逆差δ（即风险大小）。

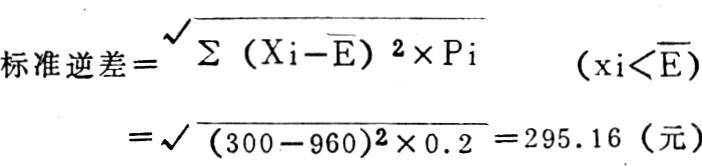
②计算标准逆差率（即风险程度）。

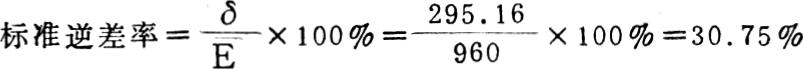
③计算应得风险价值。

笔者的计算结果表明，该投资方案所冒风险（2.95%）小于风险回收率（3.6%），因而是可行的。按张文介绍的方法的计算所以得出了错误的结论，是因为该文曲解了风险的正确含义，把期望值的顺差作为风险因素包括在风险程度之中，且主观地确定了风险价值系数，使风险价值失去了客观性。