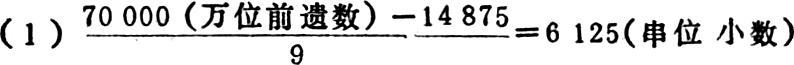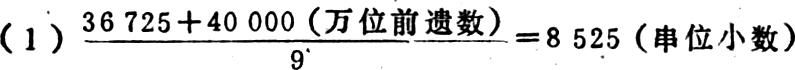会计核算是一项十分繁琐而细致的工作，在实际工作中，常会发生这样那样的帐务差错。产生差错虽是一种偶然现象，但也有一些规律可寻。现将个人从事会计工作四十余年的点滴收获以及学习运用别人的先进方法，汇编成文，供会计工作者参考。

下面分别谈几种错帐类型和查找方法：

（一）大小数——串一位

大小数差错就是某个数字，在记帐或计算时，把位数搞错了而造成的大小数差错。串一位大小数的特点是，其差数是小数的9倍，小数乘10即是大数。如980误记成98，差数882，被9除得98，即是串一位的小数，大数是980。

用9除差数，判断其能否除尽，可以采取两种简便方法：

一是“加实除九法”。即差错数的有效数相加被9除。

二是“消九法”。即差数的实数能凑够9者均予划消，最后没有余数，即证明可以被9除尽。

（二）大小数——串两位

串两位大小数的特点是，差数同时可以被9和11除尽，用99除，，其商数即小数，小数的100倍就是大数。如91800误记918，差数90882，验证如下：

（1）用9除，可采用“加实除9法”，（9+8+8+2）÷9=3，

（2）用11除，可采用下列公式：（个位+百位+万位+……）-（十位+千位+十万位+……）=0或11.即（2+8+9）-（8+0）=11。为什么这样计算呢？因为个、百、万位都是“单数位”，分别用11除，其余数均与本身数相同；而十、千、十万位，都是“双数位”，分别用11除，其余数都是本身数和11的差数；二者相减就是把“单数位”的余数和“双数位”的欠数凑成11的倍数，如相减后为0或11，说明可以被11除尽。

（三）大小数——串三位

串三位大小数的特点是，差数可以同时用9和111除尽，用999除差数，其商数即是小数，大数则是小数的1000倍。如7128000误记7128，差数7120872，用9和111都能除尽。

求小数为：7120872÷999=7128，

大数为：7128×1000=7128000。

（四）相邻数跳数差错

相邻数跳数差错，就是有两个相同数和一个不相同的邻数，由于记帐或计算时心急，造成跳数而形成的串数差错。如：221误为211，差数是10，被10除商1，即可判断相邻跳数的差数是1；如商2则相邻互串的差数为2。余类推，如：

此类差错有时发生在数字中间，可同样运用上述方法查找。如8722150误为8721150，差数是1000，被10除得100，可在百位与千位数中去找跳数差错。

（五）三位数颠倒互串

三位数颠倒互串就是一个由两位实数组成的三位数，因记载或计算时互相颠倒串位而造成的差错。其特点是差数用9除不尽，但差数的个位数乘9等于百、十位数，互串的两个实数之差，正是差数的个位数。如181误为818，差数是637，个位数乘9等于63，而8和1相差7，正好是个位数。类似情况如：

此类差错有时发生在数字中间，同样可用上述方法查找。

如5872760误为5827260，差数为45500，则是百位以上三个数颠倒互串所致。

（六）后遗数串位

后遗数串位就是误将某数的个位数丢掉，造成不合理的大小数差错。如36826误为3682，差数是33144，其特点是差数不能被9除尽，因为它不是36820和3682的大小数，所以必须先设法找出后遗数，才能找到正确数。

公式：差数实数之和-小于差数实数之和的相近的9的

倍数=后遗数。

按上例验算如下：

（3+3+1+4+4）-9=6（即后遗数）

（33144-6）+9=3682（（小数）

3682×10+6=36826（正确数）。

为什么这样计算呢？因为36820和3682的差数是33138，（可以用9除尽），而33144比33138多6，正是后遗数造成的，所以用3682的10倍加6，才是正确数。

（七）前遗数串位

前遗数串位就是将某数的第一位数丢掉，造成不合理的大小数串位差错。其特点是差数不能用9除尽，必须先设法找出前遗数，才能按大小数规律去找出正确数。

有两种情况：一是前遗数大于第二位数时，其差数是少计算的数字，应用下列公式：

差数实数之和-小于实数之和相近的9的倍数=前遗数。

如76125误为61250，差数为14875。（1+4+8+7+5）-18=7（前遗数）。

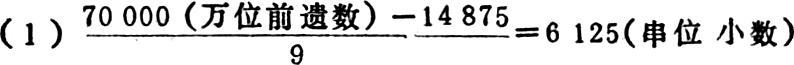
（2）6125×10=61250（串位大数——误计数）

（3）61250+14875=76125（正确数）。

为什么这样计算呢？因为：正确数是前遗数+x（串位小数），而误计数是10x（串位大数）列式如下：

70000+x-10x=14875，则9x=70000-14875，

x=6125。

6125×10+14875=76125（正确数）。

二是前遗数小于第二位数时，其差数是多计算的数字，则改用下列公式：

大于实数之和相近的9的倍数-差数实数之和=前遗数。

如48525误为85250，差数是36725，27-（3+6+7+2+5）=4（前遗数）

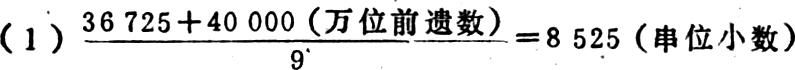
（2）8525×10=85250（串位大数——误计数），

（3）85250—36725=48525（正确数）。

为什么这样计算呢？因为：正确数是前遗数+x（串位小数），而误计数是10x（串位大数）。列式如下：

10x-（40000+x）=36725，则9x=36725+40000，

x=8525。

8525×10-36725=48525（正确数）。

×××

以上几种帐务差错类型和查找方法，只是抛砖引玉，可能有不周之处，请同志们提出批评更正意见。