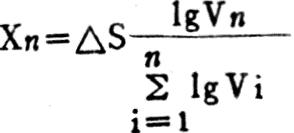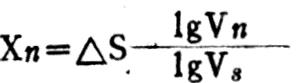摘要:
在经济活动分析中,若干个因素同时变化,影响某一分析对象的总体数量发生变化时,除了在假定其他因素不变的情况下某个因素变化所产生的影响量外,各因素变动差异之间也相互作用产生一个影响量,我们称其为“公共影响量”。
由于公共影响量产生作用的各方都是变量,它们应是以动态形式相互发生作用的。一个因素由基期到报告期之间没有各阶段的实际数据,但它却是由无限密集的阶段逐步变化的,我们要了解各阶段的情况,就必须以各个因素的最终变化速度为依据,划分为任何有限的阶段数,再根据假定的阶段数求出平均环比发展速度,从而确定每个阶段因素的变化现状及其与其他因素同一阶段发生作用的轨迹。这一方法可叫做“动态函数法”,用坐标图表示为:(图见右栏上)
“动态函数法”把座标中代表“公共影响量”的面积分割成两个曲面三角形,其计算比较复杂,在工作中推广可能会有一定困难。我们在实践中总结出一种简易算法,即以各因素变化速度的常用对数之间的比例进行分配,其计算结果同样准确。计算公式是:


在经济活动分析中,若干个因素同时变化,影响某一分析对象的总体数量发生变化时,除了在假定其他因素不变的情况下某个因素变化所产生的影响量外,各因素变动差异之间也相互作用产生一个影响量,我们称其为“公共影响量”。
由于公共影响量产生作用的各方都是变量,它们应是以动态形式相互发生作用的。一个因素由基期到报告期之间没有各阶段的实际数据,但它却是由无限密集的阶段逐步变化的,我们要了解各阶段的情况,就必须以各个因素的最终变化速度为依据,划分为任何有限的阶段数,再根据假定的阶段数求出平均环比发展速度,从而确定每个阶段因素的变化现状及其与其他因素同一阶段发生作用的轨迹。这一方法可叫做“动态函数法”,用坐标图表示为:(图见右栏上)
“动态函数法”把座标中代表“公共影响量”的面积分割成两个曲面三角形,其计算比较复杂,在工作中推广可能会有一定困难。我们在实践中总结出一种简易算法,即以各因素变化速度的常用对数之间的比例进行分配,其计算结果同样准确。计算公式是:

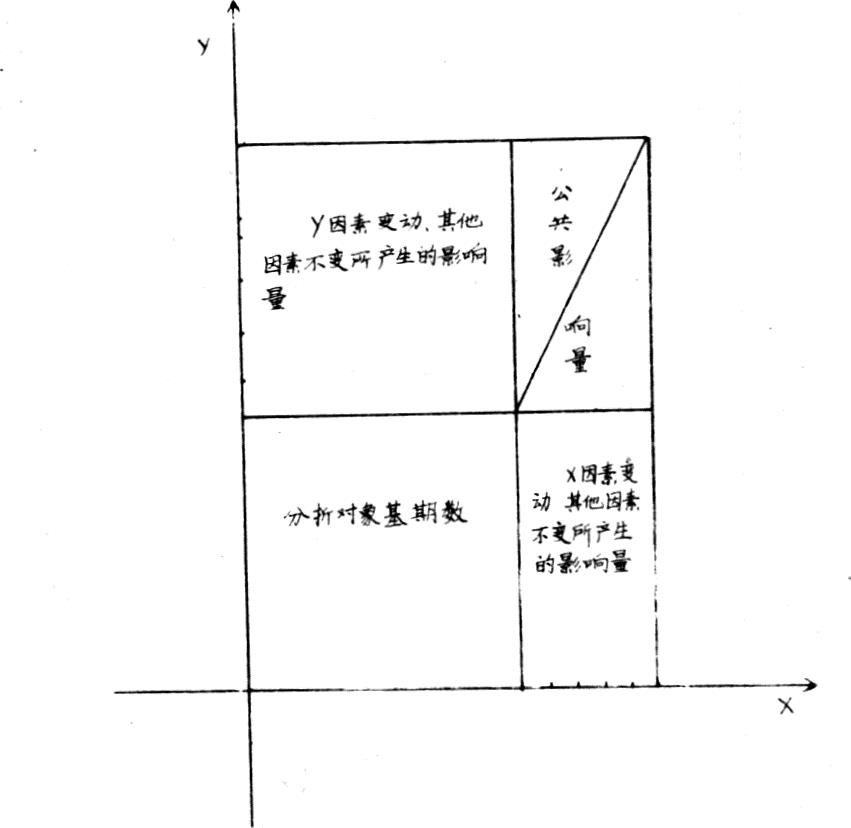
即:
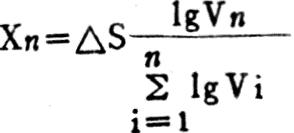
由于“各因素变化速度的常用对数之和”等于分析对象变化速度的常用对数,所以上述公式又可写为:

即:
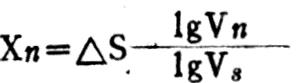

△S=X4+XB+Xc=330.3995337+(-281.0082602)+510.6087265=560
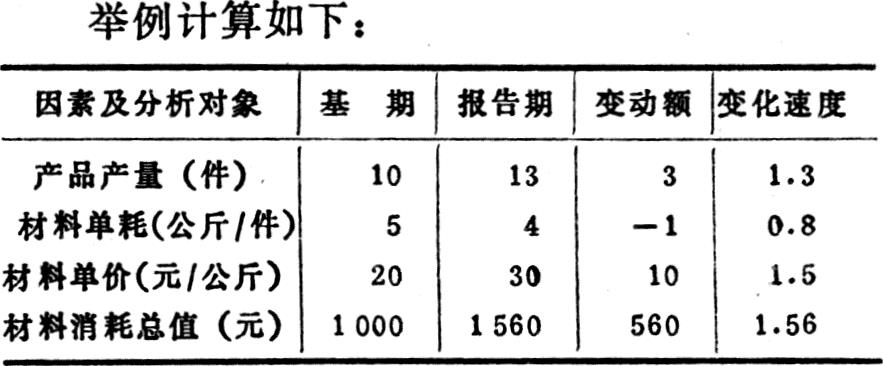
有一个问题需特别说明,就是因素之间须是相乘关系,如上例产品产量、材料单耗、材料单价三个因素对材料消耗总值的影响,它们之间就是相乘的关系。如果是几对“两因素”的组合,如销售额、毛利率、费用率、税金率对利润的影响就是三对“两因素”则应按“两因素的计算方法分别进行。
 当前位置:首页 > 用户服务 > 过刊查询 > 财务与会计过刊查询 > 《财务与会计》1987年第04期 > 财务与会计1987年第04期文章 > 正文
当前位置:首页 > 用户服务 > 过刊查询 > 财务与会计过刊查询 > 《财务与会计》1987年第04期 > 财务与会计1987年第04期文章 > 正文 京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号 京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号