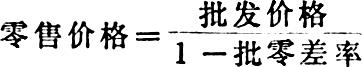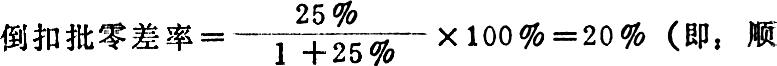摘要:
读了《财务与会计》1986年第二期黄运华等同志《如何准确计算批发金额》一文(以下简称《计算》),有些不同看法,提出来与作者商榷。
1.《计算》作者以零售价格和顺加批零差率,用加价法和扣价法两个计算公式,分别计算批发价格。因其结果不同,从而得出了扣价法计算公式(文中称之为“顺扣”法公式)是错误的,并认为该公式“应该否定”。笔者不敢苟同这种意见。
商品价格有两种计算方法,即加价法和扣价法。例如,零售价格一般是在批发价格的基础上,外加批零差价制定的,即为加价法。其计算公式为:
零售价格=批发价格×(1+批零差率)
或批发价格=零售价格÷(1+批零差率)
大部分商品的价格均采用此法计算的。
另一种是以内扣的形式来计算价格的,有少数商品(如手表)及全国一个价的商品,往往先规定零售价格,然后根据零售价格及倒扣批零差率来计算批发价格,即为扣价法。其计算公式为:
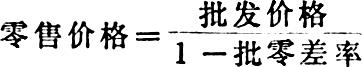
或批发价格=零售价格×(1-批零差率)
上述两个公式中所采用的批零差率,其计算基础是不同的。批零差率是批零差价与...
读了《财务与会计》1986年第二期黄运华等同志《如何准确计算批发金额》一文(以下简称《计算》),有些不同看法,提出来与作者商榷。
1.《计算》作者以零售价格和顺加批零差率,用加价法和扣价法两个计算公式,分别计算批发价格。因其结果不同,从而得出了扣价法计算公式(文中称之为“顺扣”法公式)是错误的,并认为该公式“应该否定”。笔者不敢苟同这种意见。
商品价格有两种计算方法,即加价法和扣价法。例如,零售价格一般是在批发价格的基础上,外加批零差价制定的,即为加价法。其计算公式为:
零售价格=批发价格×(1+批零差率)
或批发价格=零售价格÷(1+批零差率)
大部分商品的价格均采用此法计算的。
另一种是以内扣的形式来计算价格的,有少数商品(如手表)及全国一个价的商品,往往先规定零售价格,然后根据零售价格及倒扣批零差率来计算批发价格,即为扣价法。其计算公式为:
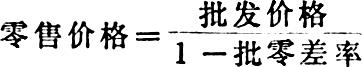
或批发价格=零售价格×(1-批零差率)
上述两个公式中所采用的批零差率,其计算基础是不同的。批零差率是批零差价与批发价格或零售价格的比率。在加价法公式中所用的是顺加批零差率,它是以批发价格为基础计算的。其计算公式为:

而扣价法公式中所用的是倒扣批零差率,又叫零批差率。它是以零售价格为基础计算的。其计算公式为:

因按加价法公式计算的价格基数较低,而按扣价法公式计算的价格基数较高,由于两个公式所用的批零差率的计算基础不同(一个用批发价格为基础,一个用零售价格为基础),虽然用相同的批零差率,分别以两个公式计算价格,其数值必然是不同的。用加价法公式计算的价格,要比扣价法公式计算的价格为小。
《计算》作者以同一批零差率用两个公式验算,由于结果不等,就认为扣价法公式(文中称之为“顺扣”公式)是错误的而应该否定,这是没有理由的。作者的验算数据,恰恰证明了扣价法公式的正确性。《计算》作者产生这种误解,主要是对加价法和扣价法两个公式之间的内在联系没有搞清楚。其实,通过换算就可以使其得到统一。其换算公式如下:

例如,某种商品的批发价格1.20元,规定顺加批零差率为25%,则
零售价格=1.20元×(1+25%)=1.50元。如要按扣价法公式验算其批发价格。应将顺加批零差率先换算成倒扣批零差率:
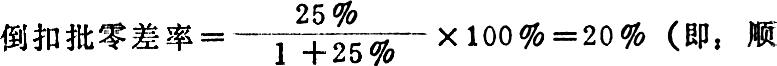
加批零差率25%相当于倒扣批零差率20%),然后代入公式,则:按扣价法公式计算的批发价格=1.50×(1-20%)
=1.20元
两个公式计算结果就一样了。关键在于,在制定零售价格时,要分清哪些商品是顺加的批零差率,哪些商品是按零售价格倒扣的批零差率。
二、《计算》作者所设计的“批发对应相乘数”,实际上是加价法(文中称之为“倒扣”法)公式

也就是把计算批发价格由除式计算变为乘式计算。这样,计算起来似乎要简便些。但“对应相乘数”因只保留一位小数,在换算时已产生了人为的误差因素(换算时的差错暂不管它,例如,批发回扣点12%时,“对应相乘数”应为89.3而误为89.2;13%时,应为88.5误为88.4;16%时,应为86.2误为86.1;20%时,应为83.3误为83.4),因此,在实际应用时,必将产生较大的误差值。经笔者测算,其误差如下表:
根据上表所列测算的误差值,如企业在发生的批发额较大的情况下,按批发价格=零售价格×批发对应相乘数(%)计算的金额,其中的误差绝对值必然也较大。为了减少误差,笔者认为,“对应相乘数”应至少保留二位小数为宜,这样可大大提高其准确度。
如用加价法由零售价格计算批发价格时,也可用下列公式计算:

这样完全可以避免误差,如用扣价法时,则直接用下列公式计算,就更为简便:
批发价格=零售价格×(1-倒扣批零差率)
另外《计算》一文中对批零差率的提法也很不一致。有的说成“批发点子”、协商扣率”,有的又说是“批零差15点”、“加10点计为零售价”等等,令人不知所云。

 京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号网络出版服务许可证:(署)网出证(京)字第317号 京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号
京公网安备 11010802030967号
互联网新闻信息服务许可证:10120240014
网络出版服务许可证:(署)网出证(京)字第317号