转移支付均衡状态的度量

经济政策的实施必须对其效果进行分析。财政转移支付的目标是实现公共服务的大致均等，换言之，横向公共服务不均衡需要财政转移支付予以解决。在财政转移支付之前，需要度量地方横向公共服务均衡的状态，以便制定相应的转移支付策略；在财政转移支付之后，需要度量地方横向公共服务均衡的变化情况，以便检验转移支付对均衡产生积极或消极的影响。对地方横向公共服务均衡状态的度量，不但是财政转移支付的重要政策依据，而且是财政转移支付均衡效果客观评价的重要指标，是规范化财政转移支付制度的重要内容。在财政转移支付中，如何对横向均衡状态进行科学的度量呢？

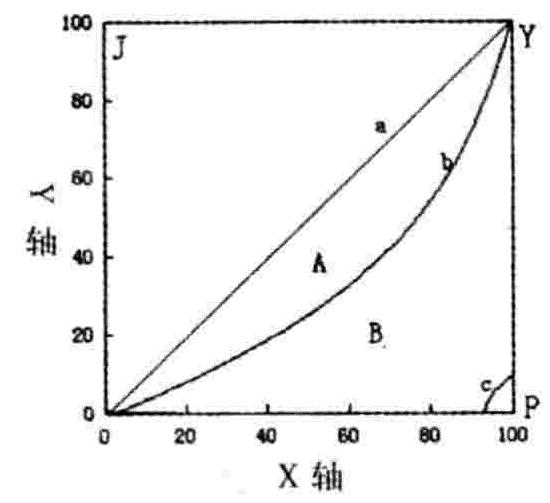
1905年，美国统计学家洛伦茨首次提出了用以描述社会收入平均程度的洛伦茨曲线分析方法。根据洛伦茨曲线进行计算，判断收入分配平均程度的指标是基尼系数。这种方法可以用图3来表明收入分配情况。图中，OJ表示收入百分比，OP表示人口的百分比，联结两对角线的直线（45度线）是绝对平均曲线（a），线上任何一点至纵轴和横轴的距离都是相等的。对角线上的任何一点表示：总人口中每一定百分比的人口所拥有的收入，在总收入中也占一定的百分比，如果社会收入分配情况正是如此，那就说明社会收入是绝对平均的。OPY线是绝对不平均曲线（C）。这条线表示：社会成员中，除一人以外，其余的人的收入都是零，而这最后的一人则得到收入的全部。实际收入分配曲线（b）介于绝对平均曲线（a）与绝对不平均曲线（c）之间。在这条曲线上，除了起点（o点）与终点（y点）以外，任何一点都是两轴的距离不相等。实际收入分配曲线中的每一点都表明：占总人口的一定百分比的人口拥有的收入在总收入中所占的百分比。实际收入分配曲线与绝对平均曲线越接近，社会收入分配越接近平均；反之，这两条曲线差距越大，社会收入分配越不平均。基尼系数的基本原理，同样可以应用于转移支付均衡状态的度量。在不考虑支出成本差异的情况下（见图3），A表示公共服务实际支出曲线与绝对平均曲线之间的面积；B表示公共服务实际支出曲线与绝对不平均曲线之间的面积，那么，5047。如果A=0，基尼系数=0，公共服务绝对平均；如果B=0，基尼系数=1，公共服务绝对不平均，基尼系数总是在0与1之间。基尼系数越小，越接近于公共服务均等；基尼系数越大，公共服务越不均等。

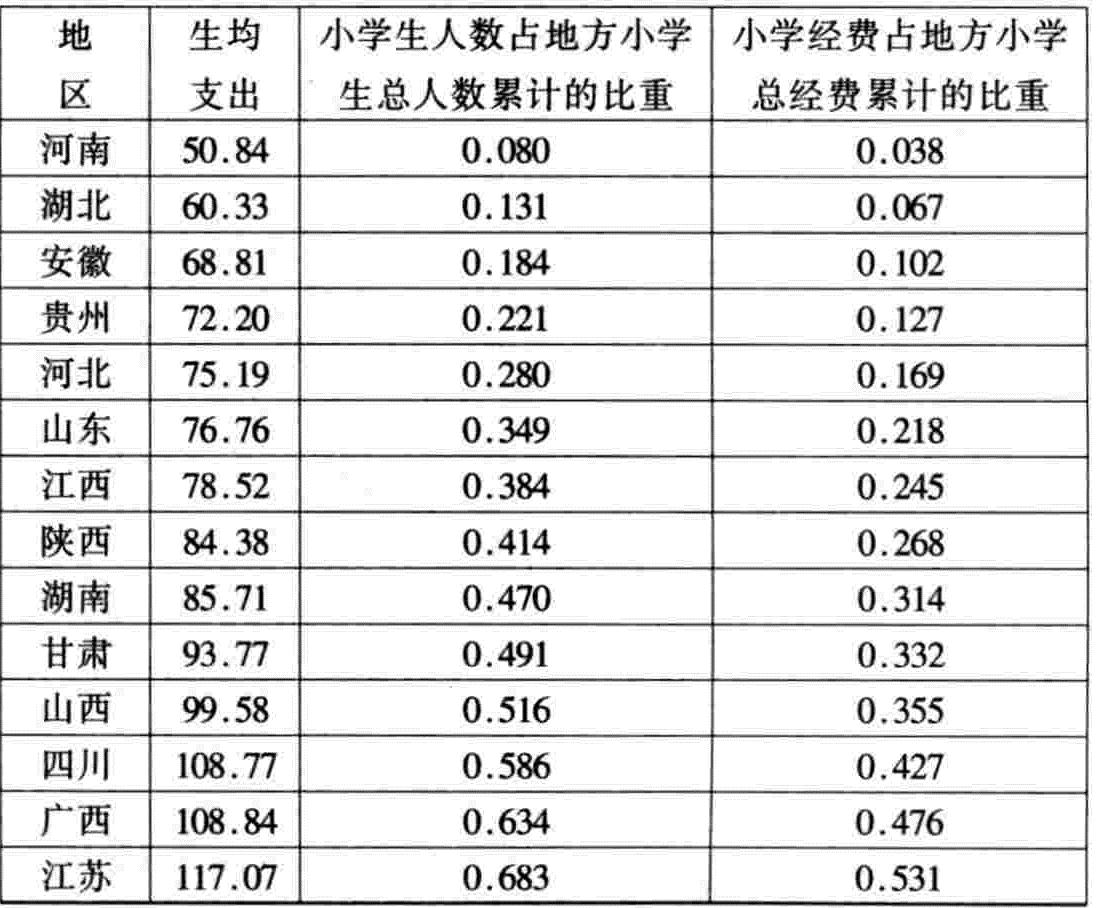
例如，国家财政对小学支出均等化实行专项转移支付，以改善贫困地区小学教育的投入，根据1991年各地小学生经费支出横截面数据可以构造如下两个变量（见下表）：（1）各地小学生人数占地方小学生总人数累计的比重；（2）各地小学经费占地方小学总经费累计的比重。

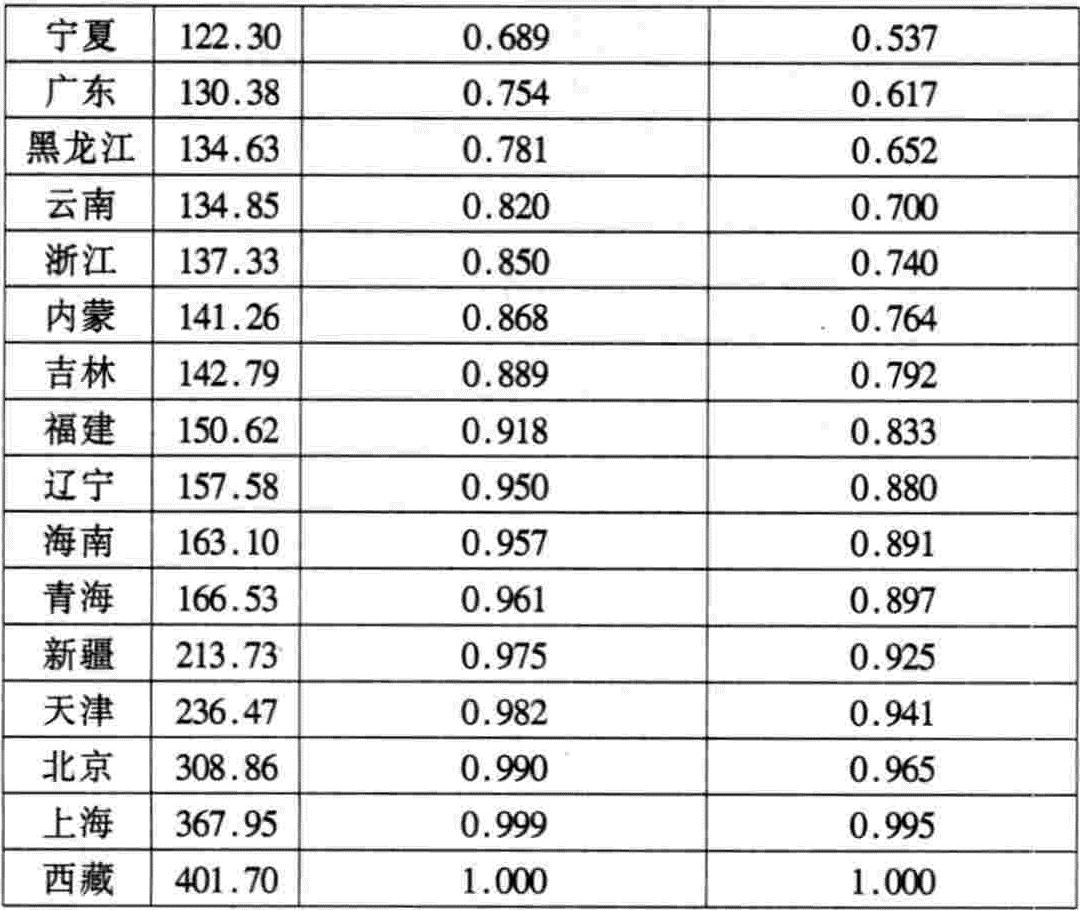
以“各地小学生人数占地方小学生总人数累计的比重”为横坐标、“各地小学经费占地方小学总经费累计的比重”为纵坐标，在一个单位正方形内描点，通过这些点连接为一条曲线，按单位正方形的面积等于1计算，这一不均度将在（0，1/2）上变化。为方便起见，把对角线右下方的这块面积算作1，不均度将扩大到（0，1）之间变化（见图4）。

通过计算，这个不均度约等于22.05%（具体计算略），也就是说，由对角线和洛伦茨曲线包围的面积为右下方三角形面积的22.05%。用同样的方法我们可以计算出1995年地方小学人均支出不均度为23.52%。通过1991年与1995年两个年度基尼系数的比较，说明地方小学公共服务支出不均度有所扩大。如果政府利用财政增量资金对某项公共服务进行转移支付，在其他条件不变的情况下，同样也可以计算出财政转移支付对该项公共服务均衡所产生的影响。由此，可以使财政转移支付与公共服务的均衡目标建立在可控的基础上，使财政转移支付制度真正走上规范、科学的轨道。（全文完）