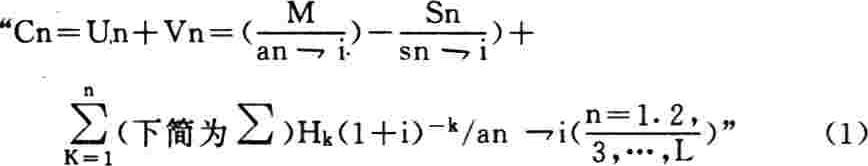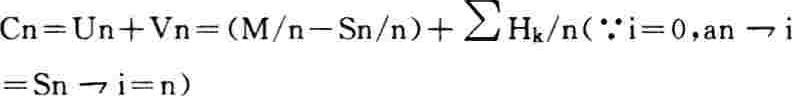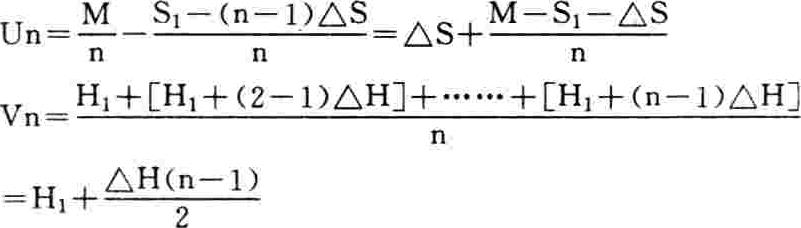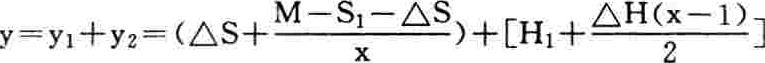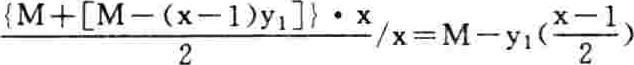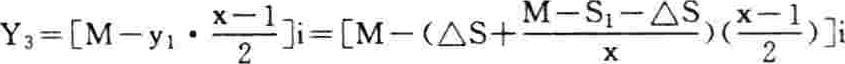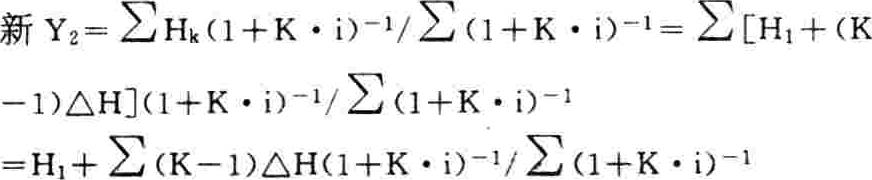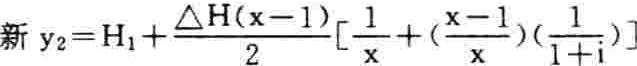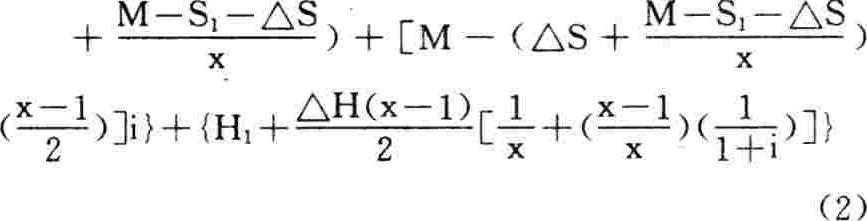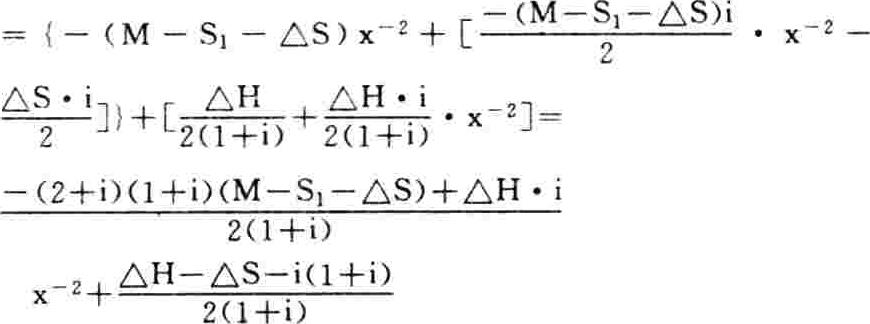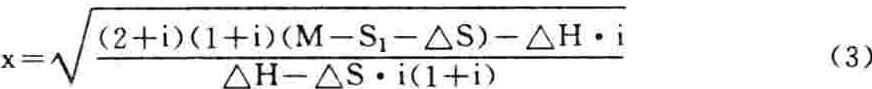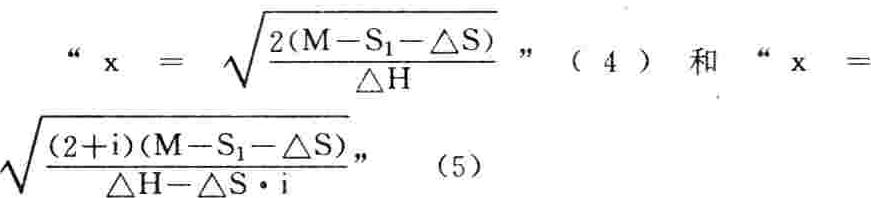目前，散见于有关译著、专论的计算固定资产经济寿命的模式，一般是“考虑资本成本（即计及利息等）和残值变动因素”的间接模式，结果较为精确，而计算也较繁复。至于其直接模式，虽然也有泰伯直接模式、早前拙论的不计利息直接模式和“修正”拙论的半计利息直接模式等，但均属粗略，局限性大，实用上较差。因此，进一步探索出与间接模式结果相当而无须繁复计算的全面直接模式，很有必要。

固定资产的经济寿命是根据固定资产使用成本的合理界限决定的使用期。经济寿命一般都比自然寿命短。拿机器设备来说，在自然寿命后期，设备由于老化和物质磨损加快，维护与使用费大量增加，超过新设备的折旧费用，继续使用原有设备，在经济上已不合理。因此，机器设备更新，通常以经济寿命为准。

我们知道，固定资产经济寿命的计算方法，尽管多种多样，但其理论根据是一致的。即：固定资产更新周期同固定资产折旧成反比例——周期长，折旧率低，周期短，折旧率高；固定资产更新周期同平均维修使用费成正比例——周期短，使用费少，周期长，使用费多；这两笔费用之和就是固定资产年均使用成本。显然，年均使用成本最低时，固定资产更新是最合理的。所以，当固定资产购价为M元，可用L年；第n年残值为Sn元[设其动态是线性的，即Sn=s1-（n-1）△S；△S为第2年起的逐年递减数]；第n年维修使用费为Hn元[设其动态也是线性的，即：Ha=H1+（n-1）△H；△H为从第2年起的逐年递增数——设备低劣化值]；以及“资本成本”即利率为i；则固定资产经济寿命的间接模式，通常是：

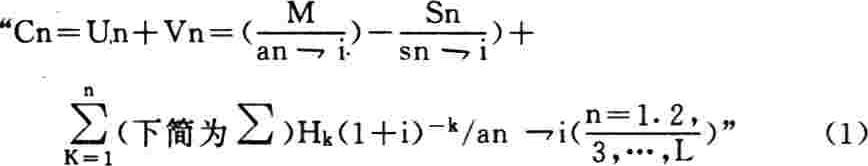
（Cn为可比平均使用成本；Un为可比年均折旧费，即括弧内数值；Vn为可比年均维修使用费，即另一个分数值；an2928i为利率为i时第n年的（下同）一元年金现值；Sn2928i则为一元年金终值；均有表可查。）

从中筛选出Ck=min{Cn}（1≤K≤L）；由此确定K（年）即固定资产的经济寿命。

为了从上列多次计算、择小筛定的间接模式推导出精确相当、一次计算的直接模式，就要把（1）式视作：年均成本（Cn）是时间（n）的函数。但是，（1）式的n是时点（年），是离散变量，Cn是相应数列，故（1）式不便据以进一步推导。尽管，绵绵不断的时间，必要时可作连续变量，但对（1）式，如不稍加简化（改复利为单利）、作适当变换的话，仍很难就此推导。故此：这特定情况下的立式推导，必须是迂回地分为三步：

第一步，先将（1）式由计及i因素退化到不计i因素。即：取i=0时

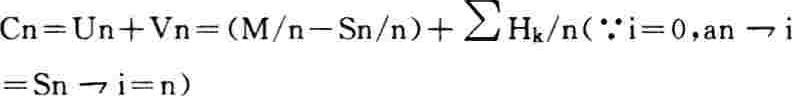
在2928之下，即得：

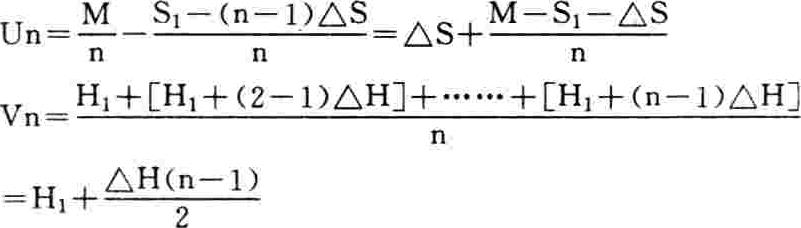
至此，不计i因素的Cn式可改写为如下的以x为自变量（一般时为连续变量）、y为因变量的函数式，当然，必要时，只要x取整数同时即作为时点（年），则y依然是年均成本数列：

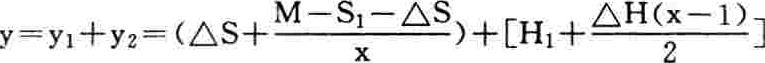
按“等差”数列求和再除以x年，得年均占用投资额为：

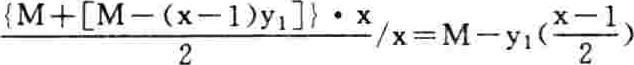
改用单利计息，故其平均利息（y3）为：

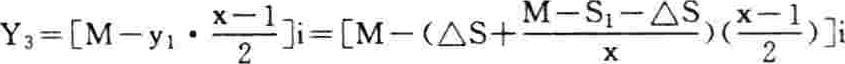
于是，稍加变换的可比年均折旧费（新y1）就是：

（2）对y2计及i因素，意即因使用维修费（终值）递增，要对y2适当折扣。

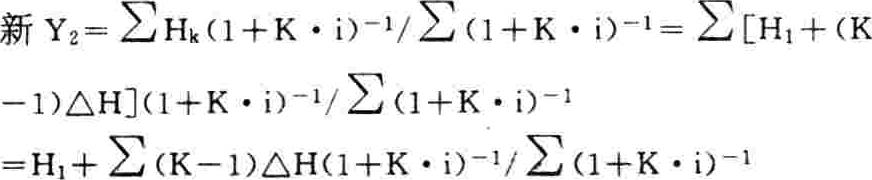
故稍加变换的可比年均维修使用费（又一新y2）是：

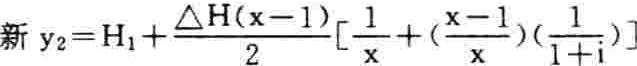
于是：计及i因素的y=新y1+新y2={（△S

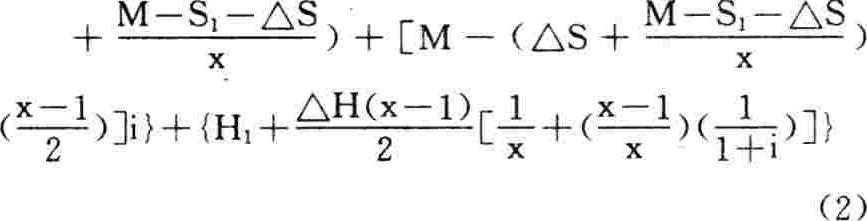
第三步，求出年均成本函数的导数（dy/dx），并解dy/dx=0，以建立直接模式。根据（2）式对x求一阶导数：3029

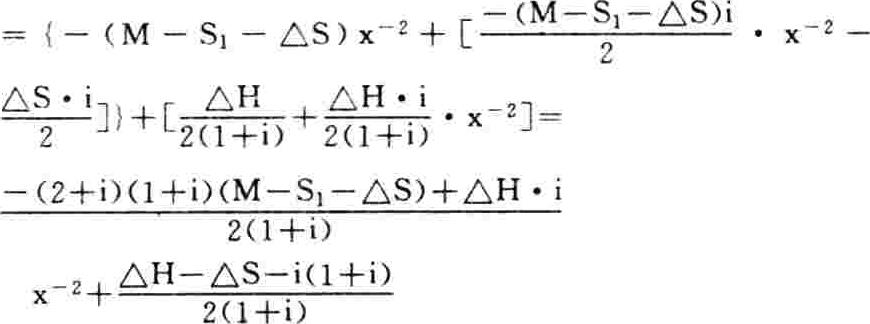
令dy/dx=0，并求解，得：

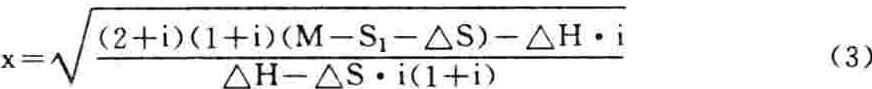
x的小数“四舍五入”后的整数（年）即固定资产经济寿命。这就是本文所要建立的与间接模式相当的直接模式。因其同样全面考虑了资本成本与残值变动两个因素，故称之为全面直接模式，以别于其他。

为表明上列模式的实用性与可信性，特作简要的算例与比较。

算例资料。某矿山厂已掌握数量最多的型号Ⅰ矿山运输汽车的有关数据为：每辆购价M=22万元，自然寿命预计L=7年；第1年残值S1=15.5万元，以后年递减数△S=2.5万元；第1年维修使用费H1=1.2万元，以后年递增数△H=0.85万元；此项利率i=6%。

算例结果。要先说明的，在计算该车的经济寿命（K）时，为便于把两个相当模式对比，且先用间接模式[前面（1）式]算出型号Ⅰ矿山汽车各年的可比年均使用成本数列是：

上列计算表明：C4值最小，故该车经济寿命K=4年。

再用全面直接模式〔即（3）式〕直接计得该车经济寿命（K）是：

由30293029

照“四舍五入”，K=4年；两相同。

至于拙论的不计利息直接模式和“修正”拙论的半计利息直接模式，则分别是⑦⑧：

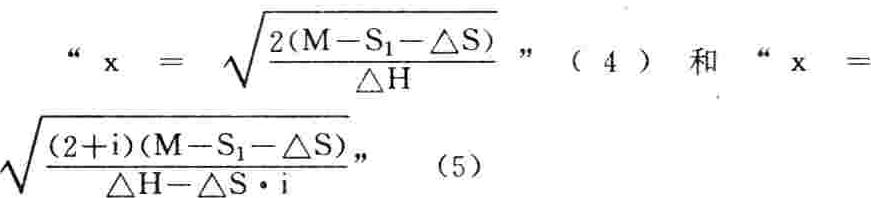
责任编辑 秦中艮