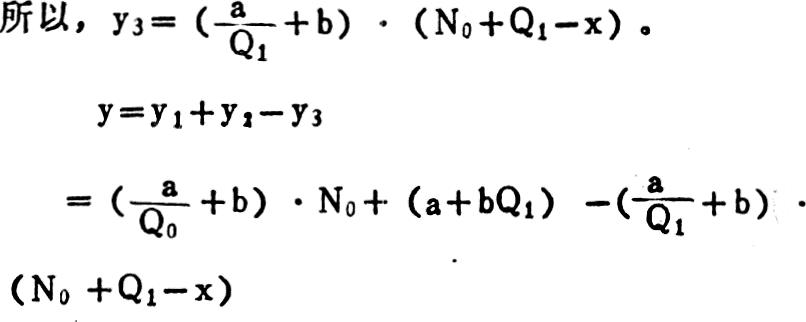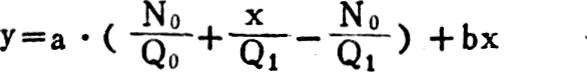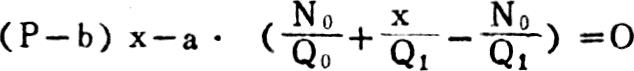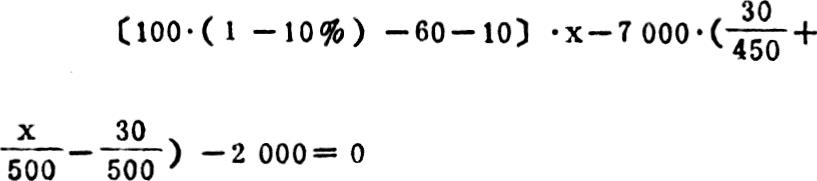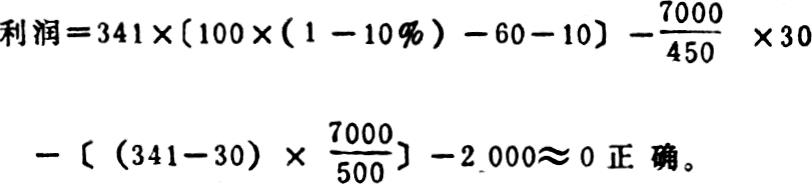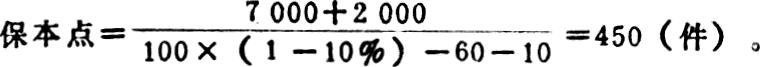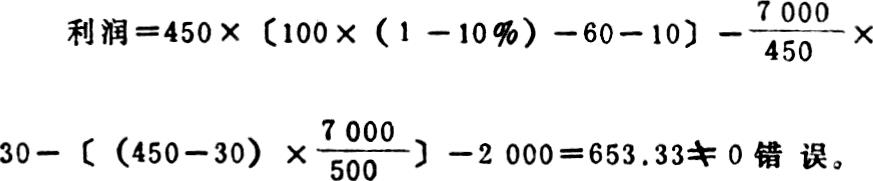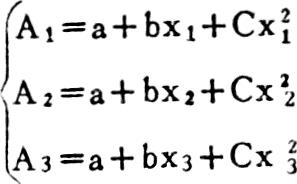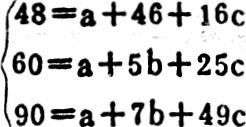保本分析揭示了企业盈亏的数量界限，在经济预测和经济决策中具有重要作用。但保本分析的理论模型是建立在一系列假设条件之下的：（1）总成本可以分为固定成本和变动成本，运用的方法是变动成本法；（2）收入线和成本线都是线性的：（3）单品种生产；（4）有关因素都是准确可知的，不存在不确定性因素。这些假定把现实的经营环境过于简单化、静止化，因而削弱了在复杂的现实经营条件下使用的有效性。本文试图探索在这些非假设条件下如何进行保本分析。多品种生产的保本分析方法已为大家所熟知，略去不谈。

一、全部成本法下的保本分析

在全部成本法下，期末库存产成品成本不但包含了变动生产成本，而且还分摊了相应份额的固定成本。当期固定成本发生额被分割成两部分，又因上期结转固定成本的加入，使得固定成本本期发生额与本期销售收入补偿额产生了较大的不一致。这样，传统的保本分析模型已不适应全部成本法的要求。

首先，研究全部成本法下销售成本与销售量的函数关系。因为在全部成本法下，销售费用已全部作为期间成本列支，故在此只研究销售生产成本，的表达式。为便于分析，设：

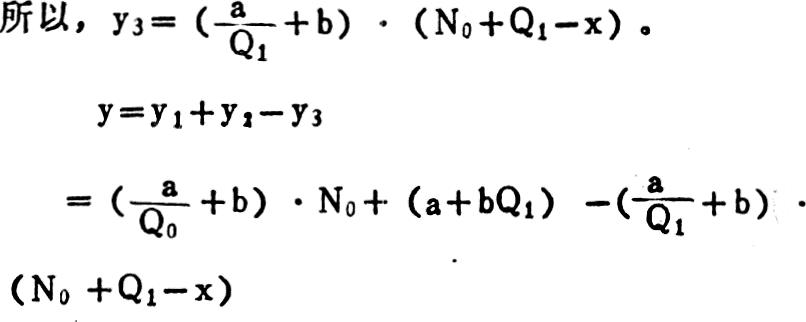
化简得：

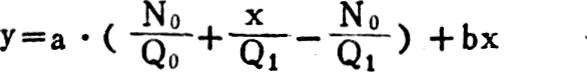
分析如下：

（1）若期初、期末无产品结存，当期生产量=当期销售量，N0=O，x=Q1，则y=a+bx，与变动成本法下销售成本表达式相同。

（4）除上述三种特殊情况外，此表达式表示全部本法下销售生产成本随销售量变化的一般函数关系。

其次，我们研究全部成本法下保本分析的模型。在一般情况下，保本点可用下式求得：

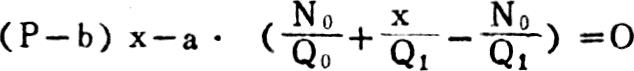
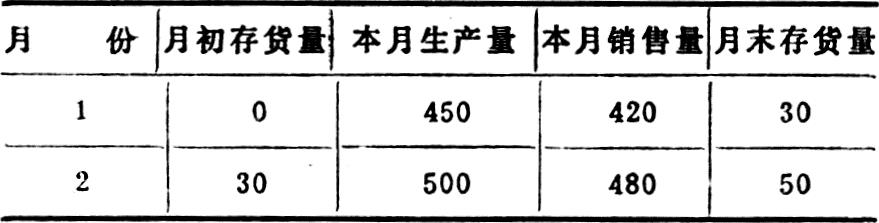
举例（例中将销售费用考虑在内）：设某企业产销一种甲产品，销售单价P为100元，单位变动生产成本b为60元，单位变动推销费用为10元，各月固定制造费用a均为7000元，固定推销费用均为2000元，产品销售税率为10%，本年1、2月份产销情况如下：

利用2月份资料代入保本分析模型：

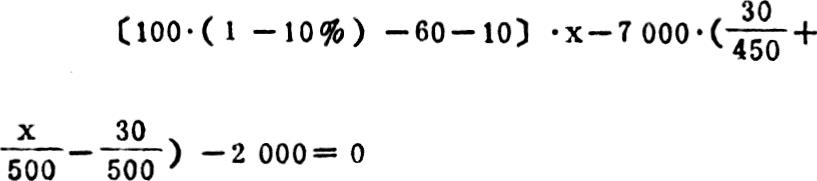
保本点x=341（件），（四舍五入取整数）。

按先进先出法验证：

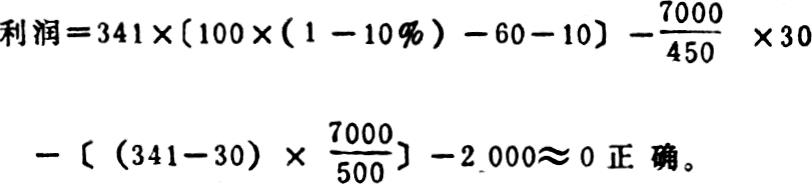
若按传统方法计算：

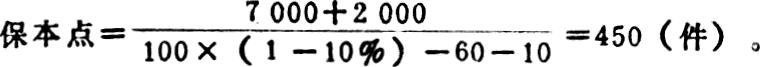
先进先出法验证：

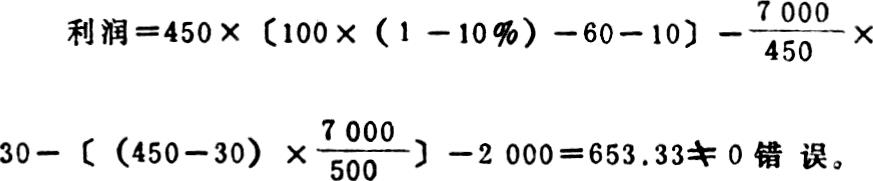
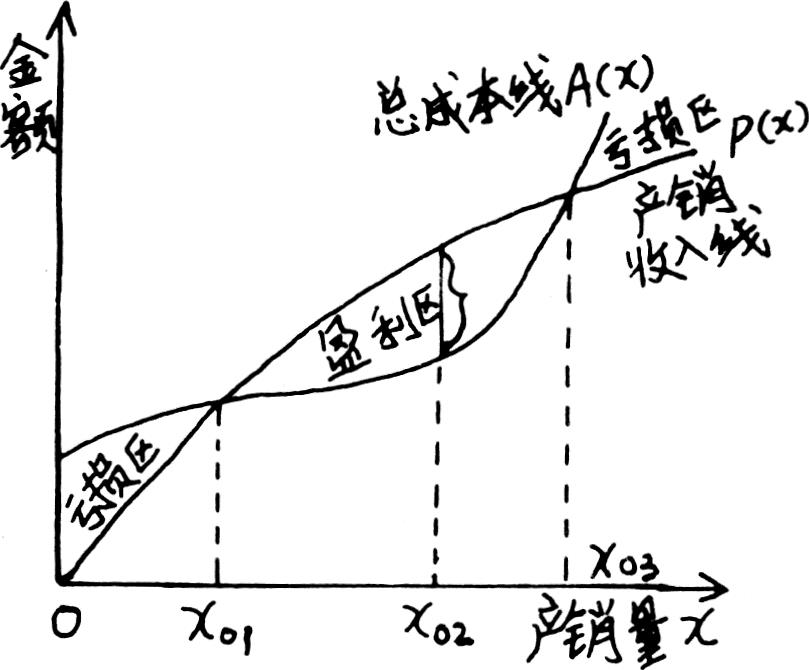
二、非线性保本分析

P（x）-A（x）=0

利润最大点可利用边际收入等于边际成本求得，亦即产销收入函数的一阶导数等于成本函数的一阶导数。即：

P’（x）-A’（x）=0

可见，进行非线性保本分析，关键在于确定收入函数P（x）和成本函数A（x）。在实际中，产销收入函数表现得最多的或保本分析中用得最多的都是线性的，即使不是这样，非线性收入函数的线性相关性也极强。所以，一般地产销收入函数可表示为线性的：P（x）=P·x。对于非线性成本函数，最多见的是二次成本函数，A（x）=a+bx+cx2（a.b.c为待定系数）。二次成本函数可根据有关数学理论确定，只要取得三个点上的产销量及对应的成本资料，就可以通过解下列方程组使之满足二次函数的一般式。

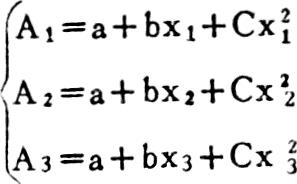
举例：某企业1，2，3月份产销量分别为4，5，7百件，其总成本分别为48，60，90万元，销售单价为15万元/百件。

产销收入函数可写成：P（x）=15x

将资料代入上述方程组：

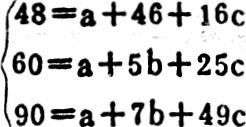
求解得：a=20，b=3，c=1，

则二次成本函数可写成：A（x）=x2+3x+20

确定保本点：15x=x2+3x+20

求解得：x1=2（百件），x2=10（百件）

确定利润最大点：

（15x）′=（x2+3x+20）’

15=2×+3

x=6（百件）

说明：当该产品的产销量大于2百件时，企业由亏变盈；在大于10百件时，由盈变亏；在产销量为6百件时，企业实现利润最大，最大利润为：15×6-（62+3×6+20）=16（万元）。

三、风险条件下的保本分析

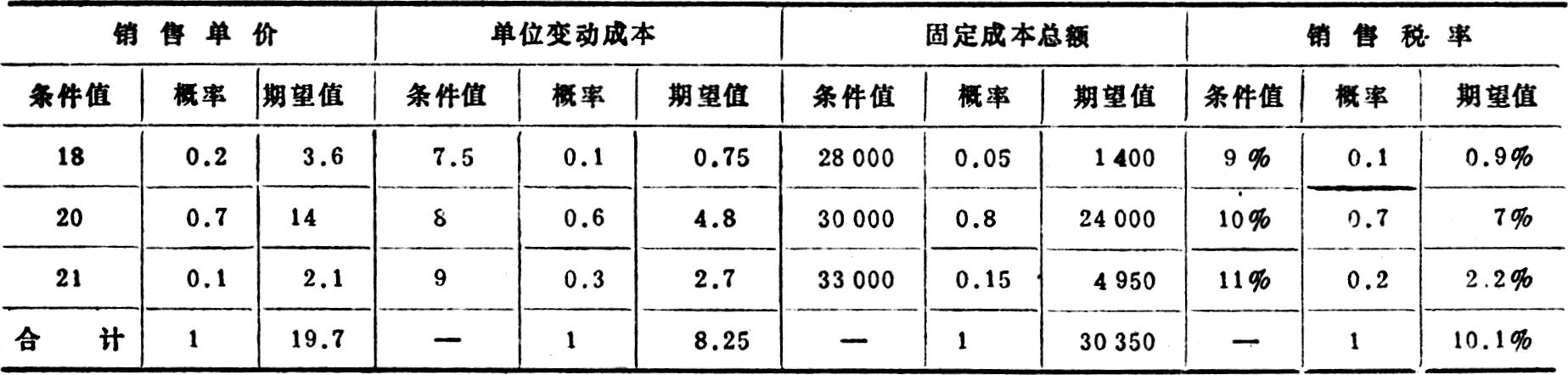
由于市场供求状况的波动、科学技术（特别是企业生产技术）的进步以及国家政策的调整，同种产品的销售单价、单位变动成本、固定成本总额和销售税率在不同的时期具有极大的不确定性。这就是保本分析中的风险。风险条件下的保本分析要充分借助概率分析方法。首先，要通过主客观判断确定各因素将来出现各种可能情况的概率；然后，计算各因素的期望值并代入传统保本点模型求得保本点期望值。