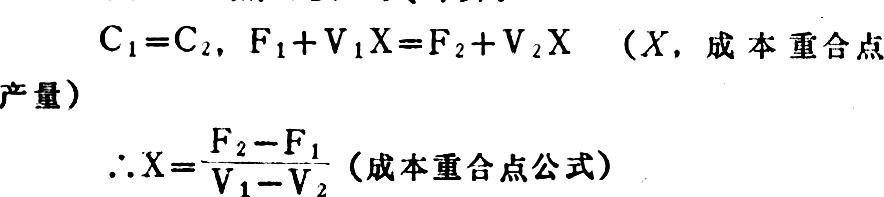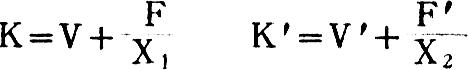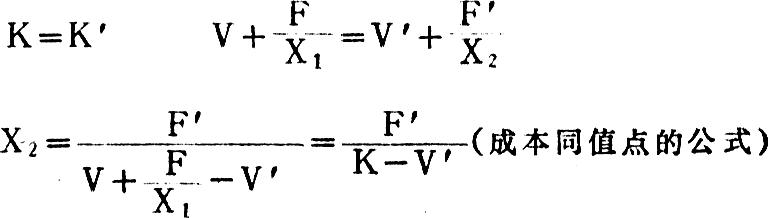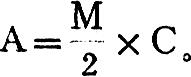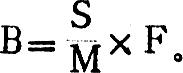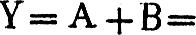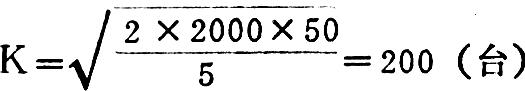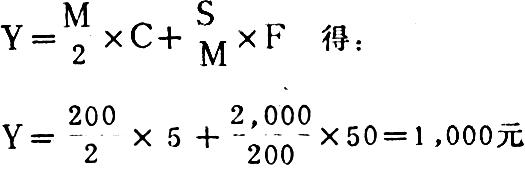成本比较分析是企业成本决策所采取的重要手段，通过比较、分析两种或两种以上方案的成本，权衡利害得失，从中选择最优方案。通常采用的成本比较基本方法有，成本重合点分析、成本同值点分析和成本最小点分析。现分别阐述如下。

一、成本重合点分析

成本是企业在一定时期内为生产产品而耗费的生产费用。从成本与产量的关系来看，成本可以分为变动成本和固定成本。一般情况下，比较方案中的固定成本和变动成本是不同的，我们把用以比较的方案归纳为以下两种类型：

现有两种方案成本，分别为C1和C2，将两者进行比较时，C2的固定成本大，而C1的单位变动成本大，在这种情况下，两者的成本线必然在产量上相交，在交点上两者的成本完全相等，这就是成本重合点。如图一所示。

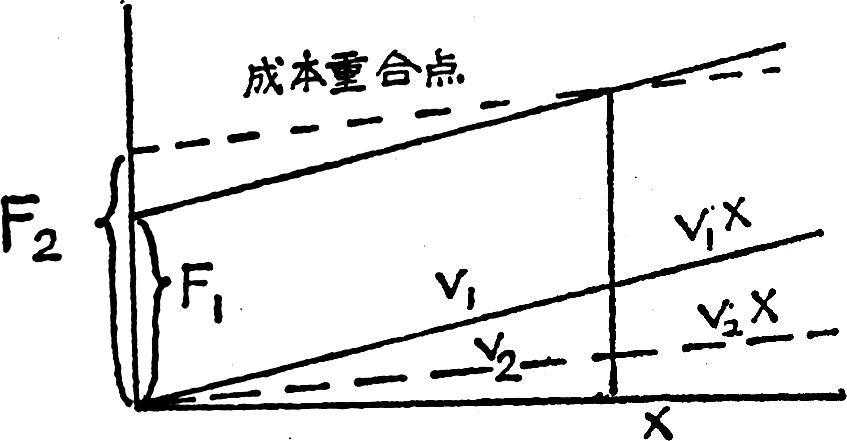
成本重合点可按下式计算：

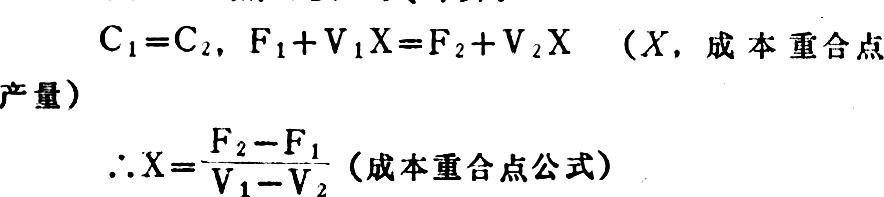
成本重合点是一个分界点，如产品产量在分界点以下，则选择固定成本小的方案；如产品产量在分界点以上，则选择固定成本大的方案。这种方法可以应用到很多方面，譬如不同生产方法的选择，不同设备的选择，企业自制零件与外购零件的选择，半成品出售或进一步加工的选择等，都可以根据这一原则进行分析。下面举一例子具体说明如下：

某企业生产洗衣机需用的小型电机，提出外购或自制两种方案进行成本决策。外购每台15元，在现有的基础上自己制造，每台需变动成本5元，若再买一台自动绕线机需5，000元，可用10年，可以减少变动成本，资料如下：

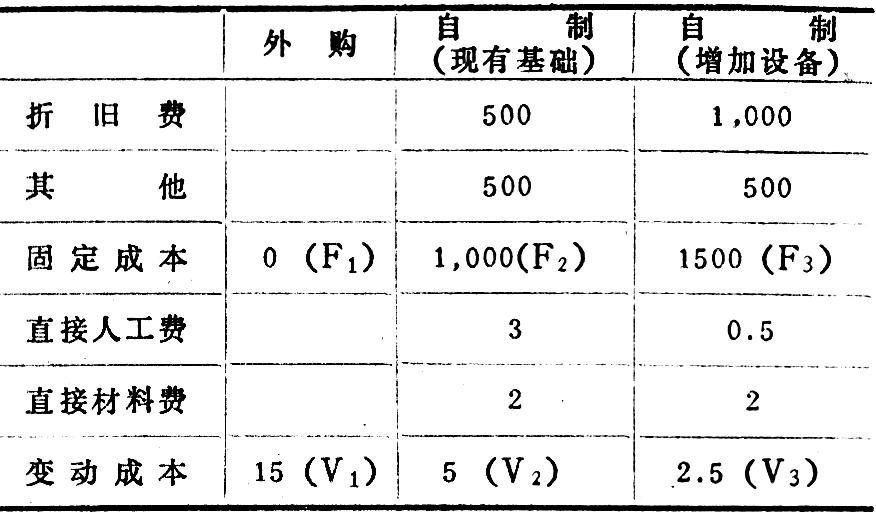
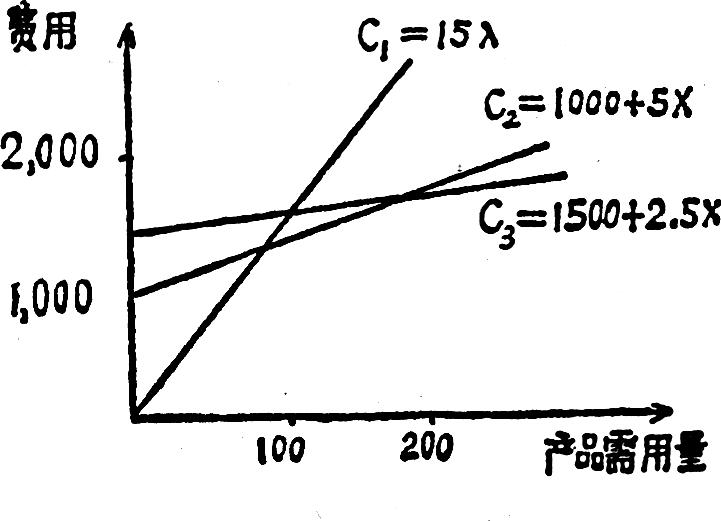
图二表明，在每年电机需用量不超过100台时，以外购最佳，所需成本最小，若超过100台不足200台时，以现有基础上自制，成本最低，超过200台，可采用增加设备方案。第三个成本重合点X3是用来比较第一备选方案的，若因人力不足等原因使第二方案不能实现时，在需用量120台以上时，可选第三方案。

二、成本同值点分析

企业在生产经营活动中，经常要遇到扩大生产规模、增加产量、降低成本的决策问题。如果企业研究某一代替方案，要求该方案的单位成本不能高于现有产品单位成本，那么，最低产量界限是多少？在此基础上，如果产量增加，将会减少多少成本？应用成本同值点分析，上述问题可以迎刃而解。

我们知道，单位成本线是一条近似于U型的曲线。因为在企业的生产经营活动中，一定产量范围内的固定成本是基本不变的，产量增加引起单位固定成本下降而使单位成本曲线向下移动；在产量超过一定数量时，企业的生产能力饱和，若要继续增加产量，势必要增加设备，增加人力，这样，单位成本曲线又呈上升趋势。单位成本变动趋势如下图所示：

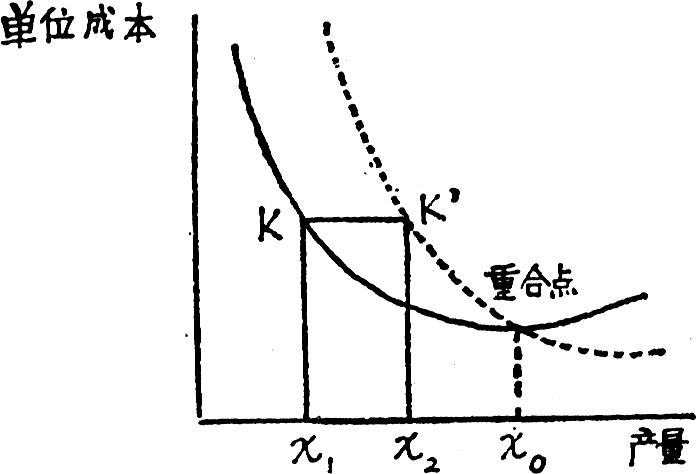
从图上可以看出，X1点产量的单位成本同X2点的单位成本是相等的。这样，就可以找出代替方案的最低必要产量。因为K等于K′，所以根据划分了的固定成本和变动成本，首先计算现有方案和代替方案的产品单位成本，然后推导出成本同值点公式：

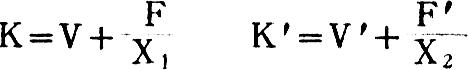
（其中，K=现有单位成本：K′=代替方案的单位成本；V、V′为单位变动成本；F、F′为全部固定成本；X1、X2为产品产量）

现有产量为X1时，其单位成本K同产量为X2的代替方案成本K′相等，则可由下式求得X2：

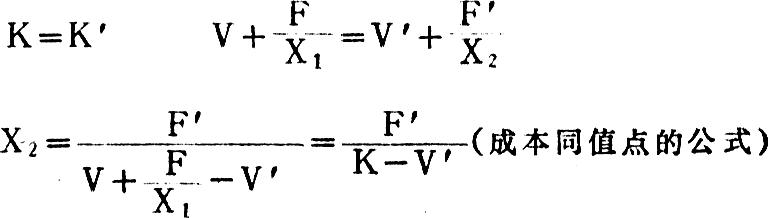
上图表明，产量如果在重合点以上，显然代替方案有利。即使产量在成本重合点以下，但只要在同值点上，仍然可以维持原来的单位成本。这样，成本同值点分析就有助于找出代替方案的最低必要产量，以便于领导者做出决策。我们还可以在计算出代替方案的最低必要产量的基础上，算出由于增加产量而使成本降低的数额。

例如，某企业由于某些因素的影响，不得不增加设备，固定成本将由目前的16，000元增加到20，000元，代替方案中的单位变动成本为15元，目前的产品单位成本为25元，产量为1，900件。那么，若采用代替方案，最低必要产量多少才能使其同现有单位成本相等？如果采用新方案，在此基础上，生产2，500件产品，能否使成本降低？

根据成本同值点公式，我们可以计算上述问题。最低必要产量X2为：

通过成本同值点分析，可以推导计算出用于决策的数据，对于现代化管理来说，是不无帮助的。

三、成本最小点分析

什么叫成本最小点？为便于理解，现以成批生产中，一次投产的最优批量为例，说明成本最小点的原理以及计算方法。

一次投产的最优批量是测算某种产品以多大批量投入生产才能使成本最低的批量，每批投入量过大或过小都会增加成本。产品投入批量与成本之间存在着两种变化规律不同的费用支出。

1.随着产品投入批量的扩大而增加的费用，如在产品的保管费用，资金占用利息等储存成本。设投入

M批量为M，则M越大，产品平均储备量2也越大，由此引起上述费用增大。以A代表它的全年总费用，则A=-M2×C。（C是每单位产品所需要的全年保管费及资金占用利息等储存成本）。

2.随着投入批量扩大而减少的费用，如一批产品投产所需要花费的准备成本F，投入批量越大，全年投入次数越少，支出的准备费也必然减少。以B代表

S它的全年总成本，则B=c-m×F。其中，S是全年该产

M品的总产量。综合以上两种费用为Y，即Y=A+B=

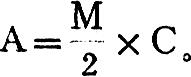
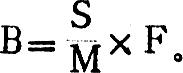
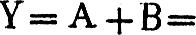
如某企业某产品的全年计划总产量为2，000单位，每储存一台半成品的储存成本为5元，投入一次所需的准备费为50元则投产的最优批量K

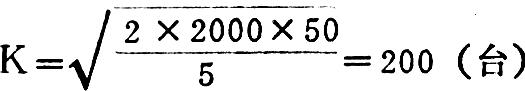
计算表明，每批投入200台，全年的成本最低，代入公式

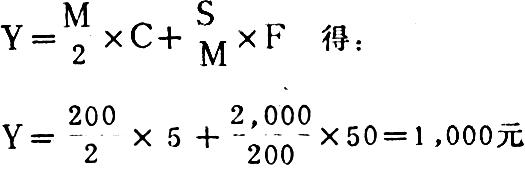
每批投入量无论大于或小于最优投入批量200台份，全年的储存成本和准备费都会高于1，000元，现将不同投入批量下的成本情况列表如下：

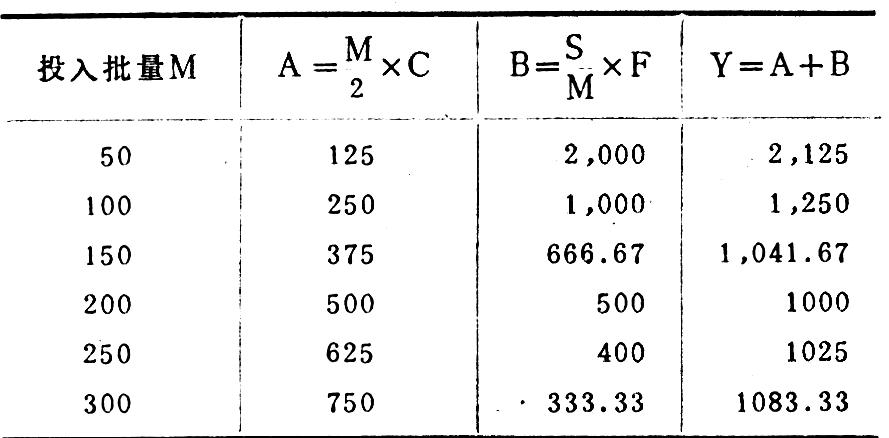
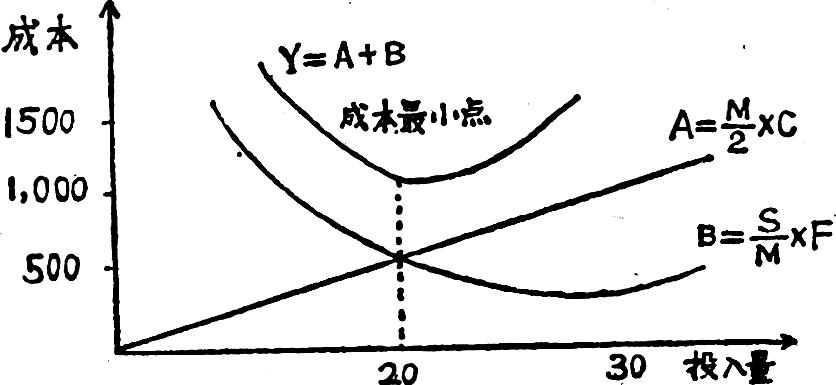
成本最小点指明了在两个成本项目发生方向不同的变化时，如何使总成本最低，这种分析，不仅可用于分析最优投入批量，而且还可以用于决定机器最优开动率，决定维修费等其他方面。